题目内容
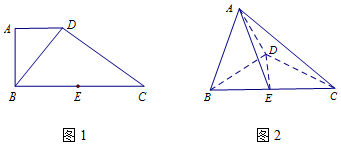
6.如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ) 若AD=1,AC与其在平面ABD内的正投影所成角的正切值为$\sqrt{6}$,求点B到平面ADE的距离.
分析 (Ⅰ)由题意结合面面垂直的性质可得BD⊥DC,有DC⊥平面ABD,进一步得到DC⊥AB,再由线面垂直的判定可得AB⊥平面ADC;
(Ⅱ)由(Ⅰ)知DC⊥平面ABD,可得AC在平面ABD内的正投影为AD,求解直角三角形得到AB的值,然后利用等积法求得点B到平面ADE的距离.
解答 (Ⅰ)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
又BD⊥DC,∴DC⊥平面ABD,
∵AB?平面ABD,∴DC⊥AB,
又∵折叠前后均有AD⊥AB,DC∩AD=D,
∴AB⊥平面ADC.
(Ⅱ)解:由(Ⅰ)知DC⊥平面ABD,所以AC在平面ABD内的正投影为AD,
即∠CAD为AC与其在平面ABD内的正投影所成角.
依题意$tan∠CAD=\frac{CD}{AD}=\sqrt{6}$,
AD=1,∴$CD=\sqrt{6}$.
设AB=x(x>0),则$BD=\sqrt{{x^2}+1}$,
∵△ABD~△BDC,∴$\frac{AB}{AD}=\frac{DC}{BD}$,
即$\frac{x}{1}=\frac{{\sqrt{6}}}{{\sqrt{{x^2}+1}}}$,
解得$x=\sqrt{2}$,故$AB=\sqrt{2},BD=\sqrt{3},BC=3$.
由于AB⊥平面ADC,AB⊥AC,E为BC的中点,
由平面几何知识得AE=$\frac{BC}{2}=\frac{3}{2}$,
同理DE=$\frac{BC}{2}=\frac{3}{2}$,
∴${S_{△ADE}}=\frac{1}{2}×1×\sqrt{{{({\frac{3}{2}})}^2}-{{({\frac{1}{2}})}^2}}=\frac{{\sqrt{2}}}{2}$.
∵DC⊥平面ABD,∴${V_{A-BCD}}=\frac{1}{3}CD•{S_{ABD}}=\frac{{\sqrt{3}}}{3}$.
设点B到平面ADE的距离为d,
则$\frac{1}{3}d•{S_{ADE}}={V_{B-ADE}}={V_{A-BDE}}=\frac{1}{2}{V_{A-BCD}}=\frac{{\sqrt{3}}}{6}$,
∴$d=\frac{{\sqrt{6}}}{2}$,即点B到平面ADE的距离为$\frac{{\sqrt{6}}}{2}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1 | B. | -1 | C. | i | D. | -i |
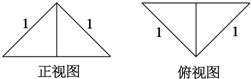 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$. 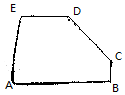 如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )
如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ | C. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | D. | -$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ |
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |

输出的结果a是( )
| A. | 120 | B. | 15 | C. | 6 | D. | 5 |
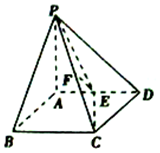 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.