题目内容
17.已知a<0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\\{y≤a(x-3)}\end{array}\right.$,若z=2x+y的最大值为8,则a=-3.分析 作出不等式组对应的平面区域,利用目标函数的几何意义即可得到结论.
解答  解:先作出不等式$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\end{array}\right.$对应的区域,
解:先作出不等式$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\end{array}\right.$对应的区域,
若z=2x+y的最大值为8,则2x+y=8,
直线y=a(x-3)过定点(3,0),
则直线2x+y=8与x-y=3相交于A,
$\left\{\begin{array}{l}{x=1}\\{2x+y=8}\end{array}\right.$得A(1,6),
同时A也在直线y=a(x-3)上,
即a(1-3)=6,
得a=-3,
故答案为:-3.
点评 本题主要考查线性规划的应用,根据目标函数的最大值,作出目标函数,求出目标函数和条件对应直线的交点坐标是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.如图所示的程序框图,若输出的结果为21,则判断框中应填入( )
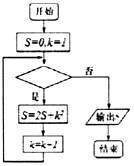

| A. | k≤2? | B. | k≤3? | C. | k≤4? | D. | k≤5? |
2.华为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别对手机的“认可”有关:
附:
K2=$\frac{n(a+d-b+c)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≧k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
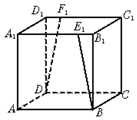 如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.
如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.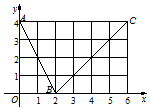 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )