题目内容
14.已知函数f(x)=lnx+$\frac{a}{x}({a>0})$.(Ⅰ) 若函数f(x)有零点,求实数a的取值范围;
(Ⅱ) 证明:当a≥$\frac{2}{e}$,b>1时,f(lnb)>$\frac{1}{b}$.
分析 (Ⅰ)法一:求出函数f(x)的导数,得到函数的单调区间,求出f(x)的最小值,从而求出a的范围即可;
法二:求出a=-xlnx,令g(x)=-xlnx,根据函数的单调性求出g(x)的最大值,从而求出a的范围即可;
(Ⅱ)令h(x)=xlnx+a,通过讨论a的范围,根据函数的单调性证明即可.
解答 解:(Ⅰ)法1:函数$f(x)=lnx+\frac{a}{x}$的定义域为(0,+∞).
由$f(x)=lnx+\frac{a}{x}$,得$f'(x)=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}$.…(1分)
因为a>0,则x∈(0,a)时,f'(x)<0;x∈(a,+∞)时,f'(x)>0.
所以函数f(x)在(0,a)上单调递减,在(a,+∞)上单调递增.…(2分)
当x=a时,[f(x)]min=lna+1.…(3分)
当lna+1≤0,即0<a≤$\frac{1}{e}$时,又f(1)=ln1+a=a>0,则函数f(x)有零点.…(4分)
所以实数a的取值范围为$({0,\frac{1}{e}}]$.…(5分)
法2:函数$f(x)=lnx+\frac{a}{x}$的定义域为(0,+∞).
由$f(x)=lnx+\frac{a}{x}=0$,得a=-xlnx.…(1分)
令g(x)=-xlnx,则g'(x)=-(lnx+1).
当$x∈({0,\frac{1}{e}})$时,g'(x)>0; 当$x∈({\frac{1}{e},+∞})$时,g'(x)<0.
所以函数g(x)在$({0,\frac{1}{e}})$上单调递增,在$({\frac{1}{e},+∞})$上单调递减.…(2分)
故$x=\frac{1}{e}$时,函数g(x)取得最大值$g({\frac{1}{e}})=-\frac{1}{e}ln\frac{1}{e}=\frac{1}{e}$.…(3分)
因而函数$f(x)=lnx+\frac{a}{x}$有零点,则$0<a≤\frac{1}{e}$.…(4分)
所以实数a的取值范围为$({0,\frac{1}{e}}]$.…(5分)
(Ⅱ)证明:令h(x)=xlnx+a,则h'(x)=lnx+1.
当$0<x<\frac{1}{e}$时,h'(x)<0;当$x>\frac{1}{e}$时,h'(x)>0.
所以函数h(x)在$({0,\frac{1}{e}})$上单调递减,在$({\frac{1}{e},+∞})$上单调递增.
当$x=\frac{1}{e}$时,${[{h(x)}]_{min}}=-\frac{1}{e}+a$.…(6分)
于是,当a≥$\frac{2}{e}$时,$h(x)≥-\frac{1}{e}+a≥\frac{1}{e}$.①…(7分)
令φ(x)=xe-x,则φ'(x)=e-x-xe-x=e-x(1-x).
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.
所以函数φ(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
当x=1时,${[{φ(x)}]_{max}}=\frac{1}{e}$.…(8分)
于是,当x>0时,$φ(x)≤\frac{1}{e}$.②…(9分)
显然,不等式①、②中的等号不能同时成立.
故当x>0,$a≥\frac{2}{e}$时,xlnx+a>xe-x.…(10分)
因为b>1,所以lnb>0.
所以lnb•ln(lnb)+a>lnb•e-lnb.…(11分)
所以$ln({lnb})+\frac{a}{lnb}>\frac{1}{b}$,即$f({lnb})>\frac{1}{b}$.…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查不等式的证明,是一道综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案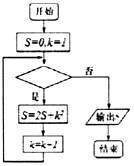
| A. | k≤2? | B. | k≤3? | C. | k≤4? | D. | k≤5? |
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≧k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
| x | 0 | 1 | 3 | 4 |
| y | a | 4.3 | 4.8 | 6.7 |
| A. | [$\sqrt{5}$,2$\sqrt{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
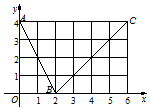 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
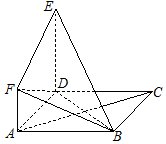 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2.
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2.