题目内容
11.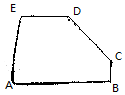 如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )
如图所示的五边形是由一个矩形截去一个角而得,且BC=1,DE=2,AE=3,AB=4,则$\overrightarrow{CD}$等于( )| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ | C. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | D. | -$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ |
分析 根据向量的加减的几何意义即可求出.
解答  解:延长BC,ED交与点O,
解:延长BC,ED交与点O,
∵BC=1,DE=2,AE=3,AB=4,
∴$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OE}$=-$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{OC}$=$\frac{2}{3}$$\overrightarrow{OB}$=-$\frac{2}{3}$$\overrightarrow{AE}$,
∴$\overrightarrow{CD}$=$\overrightarrow{OD}$-$\overrightarrow{OC}$=-$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$,
故选:C.
点评 本题考查了向量的加减的几何意义,属于基础题.

练习册系列答案
相关题目
16.已知O是坐标原点,点A(1,0),若点M(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上的一个动点,则|$\overrightarrow{OA}$+$\overrightarrow{OM}$|的取值范围是( )
| A. | [$\sqrt{5}$,2$\sqrt{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
3.若质点P的运动方程为S(t)=2t2+t(S的单位为米,t的单位为秒),则当t=1时的瞬时速度为( )
| A. | 2米/秒 | B. | 3米/秒 | C. | 4米/秒 | D. | 5米/秒 |
1.函数$f(x)=\frac{1}{{\sqrt{{x^2}-1}}}+lg({2+x})$的定义域是( )
| A. | (-2,-1) | B. | (-2,1) | C. | (-2,-1)∪(1,+∞) | D. | (-2,+∞) |
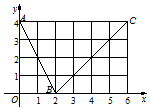 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )