题目内容
8.在一个游戏中,有两枚大小相同、质地均匀的正四面体骰子,每个面上分别写着数字1,2,3,5.同时投掷一次,记x为两个朝下的面上的数字之和,则x不小于6的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
分析 先求出基本事件总数n=4×4=16,再利用列举法求出x不小于6包含的基本事件个数,由此能求出x不小于6的概率.
解答 解:在一个游戏中,有两枚大小相同、质地均匀的正四面体骰子,
每个面上分别写着数字1,2,3,5.同时投掷一次,记x为两个朝下的面上的数字之和,
基本事件总数n=4×4=16,
x不小于6包含的基本事件有(1,5),(5,1),(2,5),(5,2),(3,5),(5,3),(3,3),(5,5),共8个,
∴x不小于6的概率为p=$\frac{8}{16}=\frac{1}{2}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
5.如图所示的程序框图,若输出的结果为21,则判断框中应填入( )
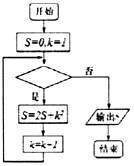

| A. | k≤2? | B. | k≤3? | C. | k≤4? | D. | k≤5? |
16.已知O是坐标原点,点A(1,0),若点M(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上的一个动点,则|$\overrightarrow{OA}$+$\overrightarrow{OM}$|的取值范围是( )
| A. | [$\sqrt{5}$,2$\sqrt{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
3.若质点P的运动方程为S(t)=2t2+t(S的单位为米,t的单位为秒),则当t=1时的瞬时速度为( )
| A. | 2米/秒 | B. | 3米/秒 | C. | 4米/秒 | D. | 5米/秒 |
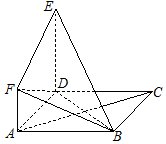 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2.
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2.