题目内容
某高校在2014年考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示,
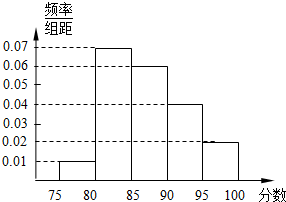
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
①已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
②若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为
,设第三组中被抽中的学生有X名获得优秀,求X的分布列和数学期望.

(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
①已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
②若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为
| 3 |
| 4 |
考点:离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由频率分布直方图能求出第3,4,5组的频率.
(2)①先求出学生甲和学生乙同时进入第二轮面试的概率,再由对立事件概率计算公式能求出学生甲和学生乙不同时进入第二轮面试的概率.
②由已知得X~B(3,
),由此能求出X的分布列和数学期望.
(2)①先求出学生甲和学生乙同时进入第二轮面试的概率,再由对立事件概率计算公式能求出学生甲和学生乙不同时进入第二轮面试的概率.
②由已知得X~B(3,
| 3 |
| 4 |
解答:
解:(1)第三组的频率为0.06×5=0.3,
第四组的频率为0.04×5=0.2,
第五组的频率为0.02×5=0.1.…3 分
(2)①设学生甲和学生乙同时进入第二轮面试为事件M:则P(M)=
=
所以学生甲和学生乙不同时进入第二轮面试的概率P(
)=1-
=
.…8 分
②由已知得X~B(3,
),且P(X=k)=
(
)k(
)3-k,k=0,1,2,3,
∴X的分布列如下:
X的数学期望EX=np=3×
=
…13 分
第四组的频率为0.04×5=0.2,
第五组的频率为0.02×5=0.1.…3 分
(2)①设学生甲和学生乙同时进入第二轮面试为事件M:则P(M)=
C
| ||
|
| 1 |
| 145 |
所以学生甲和学生乙不同时进入第二轮面试的概率P(
. |
| M |
| 1 |
| 145 |
| 144 |
| 145 |
②由已知得X~B(3,
| 3 |
| 4 |
| C | k 3 |
| 3 |
| 4 |
| 1 |
| 4 |
∴X的分布列如下:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 3 |
| 4 |
| 9 |
| 4 |
点评:本题考查频率分布直方图的求法,考查概率的计算,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意二项分布的合理运用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
圆x2+y2=4上与直线l:4x-3y+12=0距离最小的点的坐标是( )
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(-
|
设点(3,4)为偶函数y=f(x)图象上的点,则下列各点在函数图象上的是( )
| A、(-3,4) |
| B、(3,-4) |
| C、(-3,-4) |
| D、(-4,-3) |
已知向量
=(-a,2,1)与
=(1,2a,-3)垂直,则a等于( )
| m |
| n |
| A、2 | B、-2 | C、1 | D、-1 |
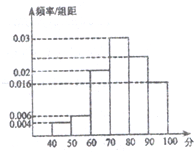 从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.
从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.