题目内容
在锐角△ABC中，角A，B，C的对边分别为a，b，c，且a=4bsinA，则cosB= ．
考点：正弦定理
专题：解三角形
分析：根据题意，由正弦定理将a=4bsinA转化为sinA=4sinBsinA，进而可得sinA的值，又由于△ABC为锐角三角形，由同角三角函数的基本关系式计算可得答案．
解答：
解：根据题意，a=4bsinA，则有sinA=4sinBsinA，
△ABC中，sinA≠0，则有sinB=
，
又由△ABC为锐角三角形，cosB=
；
故答案为：
．
△ABC中，sinA≠0，则有sinB=
| 1 |
| 4 |
又由△ABC为锐角三角形，cosB=
| ||
| 4 |
故答案为：
| ||
| 4 |
点评：本题考查正弦定理的应用，关键是利用正弦定理将a=4bsinA转化为sinA=4sinBsinA．
练习册系列答案
相关题目
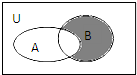设集合U={1，2，3，4，5}，A={2，3，4}，B={3，5}，则图中阴影部分所表示的集合为（ ）| A、{2，3} | B、{1，4} |
| C、{5} | D、{6} |