题目内容
设p：函数f（x）=x2-2ax+3在区间（4，+∞）上单调递增；q：loga2＜1．如果“非p”是真命题，“p或q”也是真命题，那么实数a的取值范围是 ．
考点：命题的真假判断与应用
专题：简易逻辑
分析：由函数f（x）=x2-2ax+3在区间（4，+∞）上单调递增求出a的范围，得到“非p”是真命题的a的范围，再由“p或q”也是真命题得q为真命题，求解对数不等式后取交集得答案．
解答：
解：函数f（x）=x2-2ax+3在区间（4，+∞）上单调递增，则其对称轴-
=a≤4，
由“非p”是真命题，得a＞4；
又“p或q”也是真命题，则q为真命题，则loga2＜1，
当0＜a＜1时不等式显然成立；
当a＞1时，得a＞2．
∴“p或q”也是真命题的a的范围是0＜a＜1或a＞2．
∴同时满足“非p”是真命题，“p或q”也是真命题的实数a的取值范围是{a|a＞4}∩{a|0＜a＜1或a＞2}=（4，+∞）．
故答案为：（4，+∞）．
| -2a |
| 2 |
由“非p”是真命题，得a＞4；
又“p或q”也是真命题，则q为真命题，则loga2＜1，
当0＜a＜1时不等式显然成立；
当a＞1时，得a＞2．
∴“p或q”也是真命题的a的范围是0＜a＜1或a＞2．
∴同时满足“非p”是真命题，“p或q”也是真命题的实数a的取值范围是{a|a＞4}∩{a|0＜a＜1或a＞2}=（4，+∞）．
故答案为：（4，+∞）．
点评：本题考查了命题的真假判断与应用，考查了对数不等式的解法，考查了交集及其运算，是中档题．
练习册系列答案
应用题作业本系列答案
相关题目
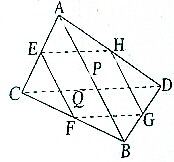如图所示，线段AB、CD所在直线是异面直线，E、F、G、H分别是线段AC、CB、BD、DA的中点．