题目内容
8.已知两点A(-1,0),B(2,1),直线l过点P(0,-1)且与线段AB有公共点,则直线l的斜率k的取值范围是( )| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | [-1,0)∪(0,1] | D. | [-1,0)∪[1,+∞) |
分析 由题意画出图形,求出P与AB端点连线的斜率,则答案可求.
解答 解:如图,
∵KAP=-1,KBP=1,
∴过P(0,-1)的直线l与线段AB始终有公共点时,
直线l的斜率k的取值范围是k≤-1或k≥1.
故选:B.
点评 本题考查直线的斜率,考查了数形结合的解题思想方法,是基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.下列函数中,在(0,+∞)为增函数的是( )
| A. | y=x2-3x+1 | B. | y=-2x+9 | C. | $y={(\frac{1}{2})^x}$ | D. | y=log2x |
3.两平行线3x-4y-12=0与6x+ay+16=0间的距离是( )
| A. | $\frac{28}{5}$ | B. | 4 | C. | $\frac{14}{5}$ | D. | $\frac{4}{5}$ |
20.已知实数a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)( )
| A. | 仅一个零点且位于区间(c,+∞)内 | |
| B. | 仅一个零点且位于区间(-∞,a)内 | |
| C. | 有两个零点且分别位于区间(a,b)和(b,c)内 | |
| D. | 有两个零点且分别位于区间(-∞,a)和(c,+∞)内 |
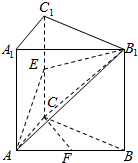 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.