题目内容
一个几何体的三视图如图所示，则这个几何体的体积是（ ）
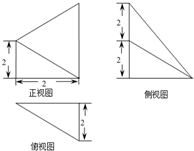
| A、1 | B、2 | C、3 | D、4 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是底面为直角梯形，高为2的四棱锥，求出它的体积即可．
解答：
解：根据几何体的三视图，得；
该几何体是如图所示的四棱锥P-ABCD，
且底面为直角梯形ABCD，高为2；
∴该四棱锥的体积为
V四棱锥=
×
×（2+4）×2×2=4．
故选：D．
该几何体是如图所示的四棱锥P-ABCD，
且底面为直角梯形ABCD，高为2；
∴该四棱锥的体积为
V四棱锥=
| 1 |
| 3 |
| 1 |
| 2 |
故选：D．
点评：本题考查了利用空间几何体的三视图求体积的应用问题，是基础题目．
练习册系列答案
相关题目
0＜a＜1，F=
，G=1+a，H=
，那么F、G、H中最小的是（ ）
| 2a |
| 1 |
| 1-a |
| A、F | B、G | C、H | D、不确定 |
为考察中学生的性别与是否喜欢某项运动之间的关系，随机抽取了某校的部分学生进行调查，并将调查数据制作成二维条形图（如图），若已知共有83名学生喜欢此项运动，且男生的喜欢比例比女生多29%，则女生中喜欢此项运动的比例是（ ）| A、35% | B、36% |
| C、64% | D、65% |
棱长为2的正方体被一平面截得的几何体的三视图如图所示，那么被截去的几何体的体积是（ ）A、
| ||
B、
| ||
| C、4 | ||
| D、3 |
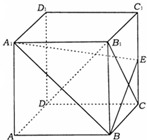长方体ABCD-A1B1C1D1中，AA1=2，BC=
如图，在?ABCD中，E是AD上的一点，且AE=AB，BE和CD的延长线交于点F，且∠BFC=35°，求?ABCD的各内角的度数．