题目内容
0＜a＜1，F=
，G=1+a，H=
，那么F、G、H中最小的是（ ）
| 2a |
| 1 |
| 1-a |
| A、F | B、G | C、H | D、不确定 |
考点：不等式比较大小
专题：不等式的解法及应用
分析：利用“作差法”比较数的大小即可．
解答：
解：∵0＜a＜1，∴G=1+a＞
=F，
H-G=
-（1+a）=
＞0，∴H＞G．
∴F、G、H中最小的是G．
故选：B．
| 2a |
H-G=
| 1 |
| 1-a |
| a2 |
| 1-a |
∴F、G、H中最小的是G．
故选：B．
点评：本题考查了“作差法”比较数的大小，属于基础题．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
一个几何体的三视图如图所示，则这个几何体的体积是（ ）
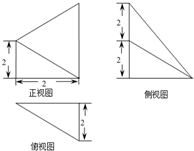
| A、1 | B、2 | C、3 | D、4 |