题目内容
已知O是空间中任意一点，A，B，C，D四点满足任意三点不共线，但四点共面，
=x
+2y
+3z
，则实数x，y，z满足关系式 ．
| OA |
| OB |
| CO |
| OD |
考点：平面向量的基本定理及其意义
专题：计算题,平面向量及应用
分析：由题意，存在m，n使得向量
=m
+n
；从而可得
=
+
=
+m
+n
=x
+2y
+3z
；化简可得（3z-n）
+（2y+m）
=（1-x-m-n）
；从而可得3z-n=0，2y+m=0，1-x-m-n=0，从而求解．
| BA |
| BC |
| BD |
| OA |
| OB |
| BA |
| OB |
| BC |
| BD |
| OB |
| CO |
| OD |
| OD |
| CO |
| OB |
解答：
解：∵A，B，C，D四点共面，则存在m，n使得向量
=m
+n
．
又∵
=x
+2y
+3z
，
∴
=
+
=
+m
+n
=x
+2y
+3z
；
而
=-
-
，
=
-
；
则（3z-n）
+（2y+m）
=（1-x-m-n）
．
因为B、D、C三点不共线，
所以OD、OC、OB不共面．
所以3z-n=0，2y+m=0，1-x-m-n=0．
解得m=-2y，n=3z，
故x-2y+3z=1．
故答案为：x-2y+3z=1．
| BA |
| BC |
| BD |
又∵
| OA |
| OB |
| CO |
| OD |
∴
| OA |
| OB |
| BA |
=
| OB |
| BC |
| BD |
| OB |
| CO |
| OD |
而
| BC |
| CO |
| OB |
| BD |
| OD |
| OB |
则（3z-n）
| OD |
| CO |
| OB |
因为B、D、C三点不共线，
所以OD、OC、OB不共面．
所以3z-n=0，2y+m=0，1-x-m-n=0．
解得m=-2y，n=3z，
故x-2y+3z=1．
故答案为：x-2y+3z=1．
点评：本题考查了平面向量的应用，属于中档题．
练习册系列答案
通城学典默写能手系列答案
相关题目
已知函数f（x）=|x2+3x|，x∈R，若函数y=f（x）-a|x-1|恰有4个零点，则实数a的取值范围为（ ）
| A、（0，1）∪[9，+∞） |
| B、（0，1）∪（9，+∞） |
| C、（1，9] |
| D、（1，9） |
如图，已知F1、F2为椭圆的焦点，等边三角形AF1F2两边的中点M，N在椭圆上，则椭圆的离心率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在三棱锥P-ABC中，PA⊥平面ABC，AB=4，BC=2，PA=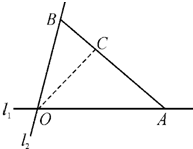
如图，在C城周边已有两条公路l1，l2在点O处交汇，且它们的夹角为75°．已知OC=（