题目内容
14.已知{an}是各项为正数的等比数列,a1+a2=20,a3=64,数列{bn}的前n项和为Sn,bn=log2an.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:对任意的n∈N*,数列{$\frac{{S}_{n}}{{a}_{n}}$}为递减数列.
分析 (Ⅰ)由题意知$\left\{\begin{array}{l}{a_1}+{a_1}q=20\\{a_1}{q^2}=64\end{array}\right.$,从而求通项公式;
(Ⅱ)化简${b_n}={log_2}{a_n}={log_2}({4^n})=2n$,从而可得${S_n}=\frac{2+2n}{2}×n={n^2}+n$,$\frac{S_n}{a_n}=\frac{{{n^2}+n}}{4^n}$;从而利用作差法判断为递减数列.
解答 解:(Ⅰ)设等比数列{an}的公比为q,
则$\left\{\begin{array}{l}{a_1}+{a_1}q=20\\{a_1}{q^2}=64\end{array}\right.$,
解得q=4或$q=-\frac{4}{5}$(舍去),a1=4;
故${a_n}=4×{4^{n-1}}={4^n}$.
(Ⅱ)证明:∵${b_n}={log_2}{a_n}={log_2}({4^n})=2n$,
∴{bn}是以b1=2为首项,以2为公差的等差数列.
∴${S_n}=\frac{2+2n}{2}×n={n^2}+n$,$\frac{S_n}{a_n}=\frac{{{n^2}+n}}{4^n}$;
∵$\frac{{{S_{n+1}}}}{{{a_{n+1}}}}-\frac{S_n}{a_n}=\frac{{{{(n+1)}^2}+(n+1)}}{{{4^{n+1}}}}-\frac{{{n^2}+n}}{4^n}$
=$\frac{1}{{{4^{n+1}}}}[{(n+1)^2}+(n+1)-4({n^2}+n)]$
=$\frac{1}{{{4^{n+1}}}}(-3{n^2}-n+2)$;
∵$\frac{-(3n-2)(n+1)}{{{4^{n+1}}}}<0$,
∴$\frac{1}{{{4^{n+1}}}}(-3{n^2}-n+2)<0$,
∴数列 $\left\{{\frac{S_n}{a_n}}\right\}$为递减数列.
点评 本题考查了对数运算的应用及等比数列与等差数列的性质,同时考查了作差法的应用,属于中档题.

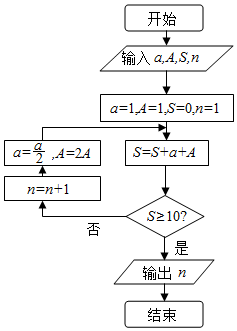 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )| A. | 4 | B. | 5 | C. | 2 | D. | 3 |
| A. | 5+i | B. | -5+i | C. | 5-i | D. | -5-i |
| A. | $\frac{7}{20}$ | B. | $\frac{1}{20}$ | C. | $\frac{5}{8}$ | D. | $\frac{2}{7}$ |
| A. | {-2} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {0,1,3} |
| A. | “p∨q为真”是“p∧q为真”的充分不必要条件 | |
| B. | 若a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$成立的概率是$\frac{1}{4}$ | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |