题目内容
4.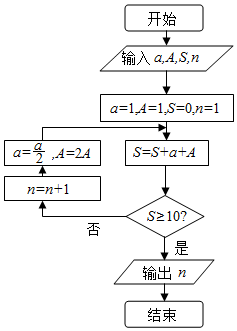 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )| A. | 4 | B. | 5 | C. | 2 | D. | 3 |
分析 模拟执行程序,依次写出每次循环得到的a,A,S的值,当S=$\frac{135}{8}$时,满足条件S≥10,退出循环,输出n的值为4,从而得解.
解答 解:模拟执行程序,可得
a=1,A=1,S=0,n=1
S=2
不满足条件S≥10,执行循环体,n=2,a=$\frac{1}{2}$,A=2,S=$\frac{9}{2}$
不满足条件S≥10,执行循环体,n=3,a=$\frac{1}{4}$,A=4,S=$\frac{35}{4}$
不满足条件S≥10,执行循环体,n=4,a=$\frac{1}{8}$,A=8,S=$\frac{135}{8}$
满足条件S≥10,退出循环,输出n的值为4.
故选:A.
点评 本题主要考查了循环结构的程序框图的应用,模拟执行程序正确写出每次循环得到的a,A,S的值是解题的关键,属于基础题.

练习册系列答案
相关题目
5.某校高三年级共有30个班,学校心理咨询室为了解同学们的心理状况,将每个班编号,依次为1到30,现用系统抽样方法,抽取6个班进行调查,若抽到的编号之和为87,则抽到的最小编号为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤1}\\{f(x-2),x>1}\end{array}\right.$,若方程f(x)-mx-1=0恰有两个不同实根,则正实数m的取值范围为( )
| A. | ($\frac{e-1}{2}$,1)∪(1,e-1) | B. | ($\frac{e-1}{2}$,1)∪(1,e-1] | C. | ($\frac{e-1}{3}$,1)∪(1,e-1) | D. | ($\frac{e-1}{3}$,1)∪(1,e-1] |
16.已知a,b∈R,且a-1+(b+2)i=0.i为虚数单位,则复数(a+bi)2在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
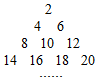 将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.
将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.