题目内容
4.下列说法正确的是( )| A. | “p∨q为真”是“p∧q为真”的充分不必要条件 | |
| B. | 若a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$成立的概率是$\frac{1}{4}$ | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |
分析 A.根据复合命题真假关系以及充分条件和必要条件的定义进行判断.
B.根据几何概型的概率公式进行计算即可.
C.根据正态分布的性质进行求解.
D.根据直线垂直的性质进行判断.
解答 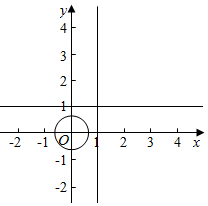 解:A.当p真q假时,满足p∨q为真,但p∧q为假,即充分性不成立,
解:A.当p真q假时,满足p∨q为真,但p∧q为假,即充分性不成立,
若p∧q为真,则p真q真,则p∨q为真即必要性成立,即“p∨q为真”是“p∧q为真”的必要不充分条件,故A错误,
B.若a,b∈[0,1],则不等式${a^2}+{b^2}<\frac{1}{4}$成立的概率是$P=\frac{{\frac{1}{4}×π×{{({\frac{1}{2}})}^2}}}{1×1}=\frac{π}{16}$.如图.故B错误
C.因为正态分布的对称轴为x=2,所以P(ξ≤0)=P(ξ≥4)=1-P(ξ≤4)=1-0.84=0.16,故C正确,
D.空间直线a,b,c,若a⊥b,b⊥c,则a∥c或a,c相交或a,c是异面直线,故D错误,
故选:C
点评 本题主要考查命题的真假判断,涉及充分条件和必要条件的判断,几何概型的概率的计算,以及正态分布等知识点,综合性较强,涉及的知识点较多.但难度不大.

练习册系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(-2,1),与$\overrightarrow{b}$=(m,3)平行,则m=( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
12.某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在[50,100]内,发布成绩使用等级制.各等级划分标准见表.规定:A、B、C三级为合格等级,D为不合格等级.
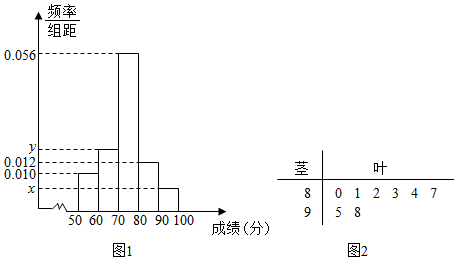
为了解该校高一年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
(I)求n和频率分布直方图中的x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中,从A、C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示所抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.
| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
(I)求n和频率分布直方图中的x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中,从A、C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示所抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.

19.若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:y=kx的距离为$2\sqrt{2}$,则直线l的斜率的取值范围是( )
| A. | $(2-\sqrt{3},2+\sqrt{3})$ | B. | $[2-\sqrt{3},2+\sqrt{3}]$ | C. | $(-∞,2-\sqrt{3})∪(2+\sqrt{3},+∞)$ | D. | $(-∞,2-\sqrt{3}]∪[2+\sqrt{3},+∞)$ |