题目内容
设定义在R上的函数f(x),对任意x,y∈R,有f(x+y)=f(x)+f(y),且当x>0时,恒有f(x)>0,
(1)求f(0);
(2)判断该函数的奇偶性;
(3)求证:x∈R时 f(x)为单调递增函数.
(1)求f(0);
(2)判断该函数的奇偶性;
(3)求证:x∈R时 f(x)为单调递增函数.
考点:抽象函数及其应用,奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:(1)由条件,令x=y=0,则f(0)=2f(0),即可得到f(0);
(2)由条件可令y=-x,则f(0)=f(x)+f(-x)=0,由奇偶性的定义即可判断;
(3)设x1<x2,则x2-x1>0,由于当x>0时,恒有f(x)>0,则f(x2-x1)>0,即有f(x2)+f(-x1)>0,再由(2)的结论和单调性的定义,即可判断.
(2)由条件可令y=-x,则f(0)=f(x)+f(-x)=0,由奇偶性的定义即可判断;
(3)设x1<x2,则x2-x1>0,由于当x>0时,恒有f(x)>0,则f(x2-x1)>0,即有f(x2)+f(-x1)>0,再由(2)的结论和单调性的定义,即可判断.
解答:
(1)解:对任意x,y∈R,有f(x+y)=f(x)+f(y),
令x=y=0,则f(0)=2f(0),
即有f(0)=0;
(2)解:函数的定义域为R,关于原点对称,
令y=-x,则f(0)=f(x)+f(-x)=0,
即有f(-x)=-f(x),
则函数f(x)为奇函数;
(3)证明:设x1<x2,则x2-x1>0,
由于当x>0时,恒有f(x)>0,
则f(x2-x1)>0,即有f(x2)+f(-x1)>0,
即f(x2)-f(x1)>0,即f(x2)>f(x1),
故x∈R时,f(x)为单调递增函数.
令x=y=0,则f(0)=2f(0),
即有f(0)=0;
(2)解:函数的定义域为R,关于原点对称,
令y=-x,则f(0)=f(x)+f(-x)=0,
即有f(-x)=-f(x),
则函数f(x)为奇函数;
(3)证明:设x1<x2,则x2-x1>0,
由于当x>0时,恒有f(x)>0,
则f(x2-x1)>0,即有f(x2)+f(-x1)>0,
即f(x2)-f(x1)>0,即f(x2)>f(x1),
故x∈R时,f(x)为单调递增函数.
点评:本题考查抽象函数及运用,考查函数的奇偶性、单调性的判断,考查解决抽象函数的常用方法:赋值法,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
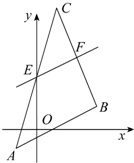 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的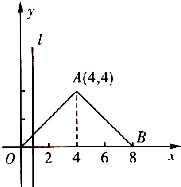 如图所示,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为(x,0).
如图所示,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为(x,0).