题目内容
已知数列{an}的前n项和为Sn,且a1=1,an+1=
Sn(n∈N*).
(1)求数列{an}的通项公式an;
(2)当bn=log
(4an+1)时,求数列{
}的前n项和Tn;.
| 1 |
| 3 |
(1)求数列{an}的通项公式an;
(2)当bn=log
| 4 |
| 3 |
| 1 |
| bnbn+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)在数列递推式中取n=n-1得另一递推式,作差得:an+1=
an(n≥2).再由a1=1求得a2,可得数列{an}从第二项起是以
为首项,以
为公比的等比数列.由此求得数列{an}的通项公式an;
(2)由bn=log
(4an+1)=log
(
)n=n,代入
,然后利用裂项相消法求数列{
}的前n项和Tn.
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
(2)由bn=log
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| bnbn+1 |
| 1 |
| bnbn+1 |
解答:
解:(1)由an+1=
Sn,得an=
Sn-1(n≥2).
两式作差得:an+1-an=
an,即an+1=
an(n≥2).
又a1=1,∴a2=
S1=
,
∴数列{an}从第二项起是以
为首项,以
为公比的等比数列.
则an=
•(
)n-2(n≥2).
∴an=
;
(2)bn=log
(4an+1)=log
(
)n=n.
=
=
-
.
∴Tn=1-
+
-
+
-
+…+
-
=1-
=
.
| 1 |
| 3 |
| 1 |
| 3 |
两式作差得:an+1-an=
| 1 |
| 3 |
| 4 |
| 3 |
又a1=1,∴a2=
| 1 |
| 3 |
| 1 |
| 3 |
∴数列{an}从第二项起是以
| 1 |
| 3 |
| 4 |
| 3 |
则an=
| 1 |
| 3 |
| 4 |
| 3 |
∴an=
|
(2)bn=log
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查了数列递推式,考查了等比关系的确定,训练了裂项相消法求数列的和,是中档题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
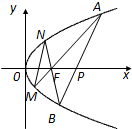 如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N.
如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N. 如图:在梯形ABCD中,AD∥BC且
如图:在梯形ABCD中,AD∥BC且