题目内容
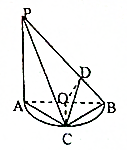 如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=
如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=| 1 |
| 4 |
 |
| AB |
(1)证明:BP⊥平面COD;
(2)求平面PAC与平面COD所成锐二面角的大小.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由线面垂直得OC⊥PA,由等腰三角形性质得OC⊥AB,从而OC⊥平面PAB,进而BP⊥OC,设BP的中点为E,连接AE由三角形中位线定理得OD∥AE,由等腰三角形性质得AE⊥BP,从而BP⊥OC,由此能证明BP⊥平面COD.
(2)以A为原点,AC为x轴,过A平行于CB的直线为y轴,AP为z轴,建立空间直角坐标系,设PA=AB=2,分虽求出平面APC的法向量和平面COD的一个法向量,由此利用向量法能求出平面PAC与平面COD所成锐二面角的大小.
(2)以A为原点,AC为x轴,过A平行于CB的直线为y轴,AP为z轴,建立空间直角坐标系,设PA=AB=2,分虽求出平面APC的法向量和平面COD的一个法向量,由此利用向量法能求出平面PAC与平面COD所成锐二面角的大小.
解答:
(1)证明:∵PA⊥平面ABC,OC?平面ABC,∴OC⊥PA.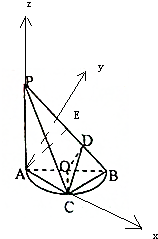
∵C是弧AB的中点,∴△ABC是等腰三角形,AC=BC,
又O是AB的中点,∴OC⊥AB.
又∵PA∩AB=A,∴OC⊥平面PAB,又PB?平面PAB,
∴BP⊥OC.
设BP的中点为E,连接AE,∵BD=
BP,∴OD∥AE,
∵PA=AB,∴AE⊥BP,∴BP⊥OC,
又CO∩OD=O,∴BP⊥平面COD.
(2)解:以A为原点,AC为x轴,过A平行于CB的直线为y轴,AP为z轴,
建立空间直角坐标系,设PA=AB=2,
由题意得A(0,0,0),P(0,0,2),C(
,0,0),B(
,
,0),
平面APC的法向量
=(0,1,0),由BP⊥平面COD,得平面COD的一个法向量为
=(-
,-
,2),
设平面PAC与平面COD所成锐二面角为θ,
cosθ=|cos<
,
>|=|
|=|
|=
,
∴θ=60°,∴平面PAC与平面COD所成锐二面角的大小为60°.

∵C是弧AB的中点,∴△ABC是等腰三角形,AC=BC,
又O是AB的中点,∴OC⊥AB.
又∵PA∩AB=A,∴OC⊥平面PAB,又PB?平面PAB,
∴BP⊥OC.
设BP的中点为E,连接AE,∵BD=
| 1 |
| 4 |
∵PA=AB,∴AE⊥BP,∴BP⊥OC,
又CO∩OD=O,∴BP⊥平面COD.
(2)解:以A为原点,AC为x轴,过A平行于CB的直线为y轴,AP为z轴,
建立空间直角坐标系,设PA=AB=2,
由题意得A(0,0,0),P(0,0,2),C(
| 2 |
| 2 |
| 2 |
平面APC的法向量
| n |
| BP |
| 2 |
| 2 |
设平面PAC与平面COD所成锐二面角为θ,
cosθ=|cos<
| n |
| BP |
| ||||
|
|
-
| ||
|
| 1 |
| 2 |
∴θ=60°,∴平面PAC与平面COD所成锐二面角的大小为60°.
点评:本题考查直线与平面垂直的证明,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养和向量法的合理运用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知{an}是各项均为正数的等比数列,且a1a2013=4,则由bn=log2an,所得数列{bn}的前2013项和为( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2013 |
如果-1,a,b,c,-4成等比数列,那么( )
| A、b=2,ac=4 |
| B、b=2,ac=-4 |
| C、b=-2,ac=4 |
| D、b=-2,ac=-4 |
若二项展开式(2x-
)n的各项系数的绝对值之和为729,则展开式中的常数项是( )
| 1 | ||
|
| A、60 | B、45 | C、35 | D、30 |
用三段论推理:“指数函数y=ax是增函数,因为y=(
)x是指数函数,所以y=(
)x是增函数”,你认为这个推理( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、是正确的 |
定义在R上的奇函数y=f(x)满足不等式:
>0(x1≠x2),若当a>0时,f(a2)+f(b2-1)<0,则
的取值范围是( )
| f(x2)-f(x1) |
| x2-x1 |
| (a+1)2+b2 |
| A、(0,2) | ||
| B、(1,2) | ||
C、(0,
| ||
D、(1,
|