题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{1-|x|,(x≤1)}\\{{x}^{2}-4x+3,(x>1)}\end{array}\right.$,若f(f(m))≥0,则实数m的取值范围是( )| A. | [-2,2] | B. | [-2,2]∪[4,+∞) | C. | [-2,2+$\sqrt{2}$] | D. | [-2,2+$\sqrt{2}$]∪[4,+∞) |
分析 令f(m)=t⇒f(t)≥0⇒$\left\{\begin{array}{l}{1-|t|≥0}\\{t≤1}\end{array}\right.$⇒-1≤t≤1;$\left\{\begin{array}{l}{{t}^{2}-4t+3≥0}\\{t>1}\end{array}\right.$⇒t≥3,再求解-1≤f(m)≤1和f(m)≥3即可.
解答 解:令f(m)=t⇒f(t)≥0⇒$\left\{\begin{array}{l}{1-|t|≥0}\\{t≤1}\end{array}\right.$⇒-1≤t≤1;
$\left\{\begin{array}{l}{{t}^{2}-4t+3≥0}\\{t>1}\end{array}\right.$⇒t≥3
下面求解-1≤f(m)≤1和f(m)≥3,
$\left\{\begin{array}{l}{-1≤1-|m|≤1}\\{m≤1}\end{array}\right.$⇒-2≤m≤1,
$\left\{\begin{array}{l}{-1≤{m}^{2}-4m+3≤1}\\{m>1}\end{array}\right.$⇒1<m≤2+$\sqrt{2}$,
$\left\{\begin{array}{l}{1-|m|≥3}\\{m≤1}\end{array}\right.$⇒m无解,
$\left\{\begin{array}{l}{{m}^{2}-4m+3≥3}\\{m>1}\end{array}\right.$⇒m≥4,
综上实数m的取值范围是[-2,2+$\sqrt{2}$]∪[4,+∞).
故选:D.
点评 本题考查了复合函数的不等式问题,换元分段求解是常规办法,也可以利用图象求解,属于难题.

练习册系列答案
相关题目
9.如图,在平行四边形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{AN}=3\overrightarrow{NC}$,则$\overrightarrow{BN}$=( )
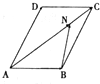

| A. | $\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$ | B. | $\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$ | C. | $\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$ | D. | $\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$ |
6.已知命题p,q,则“p或q是真命题”是“¬p为假命题”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知p是曲线$\left\{\begin{array}{l}{x=2cosβ}\\{y=\sqrt{3}sinβ}\end{array}\right.$上一点,F1,F2是该曲线的两个焦点,若△F1PF2内角平分线的交点到三边上的距离为1,则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | -$\frac{9}{4}$ | D. | 0 |
8.若a=30.6,b=log30.2,c=0.63,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<c<a | C. | a<b<c | D. | a<c<b |