如图.在平行四边形ABCD中.$\overrightarrow{AB}=\overrightarrow a.\overrightarrow{AD}=\overrightarrow b.\overrightarrow{AN}=3\overrightarrow{NC}$.则$\overrightarrow{BN}$=( )A．$\frac{3}{4}\overrightarrow b+\frac{1 题目和参考答案——青夏教育精英家教网——

题目内容

9．如图，在平行四边形ABCD中，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，\overrightarrow{AN}=3\overrightarrow{NC}$，则$\overrightarrow{BN}$=（　　）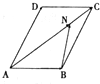

A．

$\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$

B．

$\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$

C．

$\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$

D．

$\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$

分析由已知条件得$\overrightarrow{AN}=\frac{3}{4}\overrightarrow{AC}$，再求出$\overrightarrow{AC}$，$\overrightarrow{BN}$=$\overrightarrow{AN}-\overrightarrow{AB}$，则答案可求．

解答解：∵$\overrightarrow{AN}=3\overrightarrow{NC}$，
∴$\overrightarrow{AN}=\frac{3}{4}\overrightarrow{AC}$，
又$\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{a}+\overrightarrow{b}$
则$\overrightarrow{BN}$=$\overrightarrow{AN}-\overrightarrow{AB}$=$\frac{3}{4}（\overrightarrow{a}+\overrightarrow{b}）-\overrightarrow{a}$=$\frac{3}{4}\overrightarrow{b}-\frac{1}{4}\overrightarrow{a}$．
故选：C．

点评本题考查了用一组向量来表示一个向量，考查了向量的加减运算，是基础题．

练习册系列答案

红对勾讲与练系列答案

智秦优化360度训练法系列答案

优翼优干线系列答案

绩优课堂全优达标测试卷系列答案

100分闯关期末冲刺系列答案

绩优课堂单元达标创新测试卷系列答案

名校秘题冲刺卷系列答案

神龙牛皮卷期末100分闯关系列答案

状元成才路创新名卷系列答案

优优好卷单元测评卷系列答案

相关题目

19．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的半焦距为c，（a，0）、（0，b）为直线l上两点，已知原点到直线l的距离为$\frac{{\sqrt{3}}}{4}$c，则双曲线的离心率为（　　）

$\frac{{2\sqrt{3}}}{3}$

2或 $\frac{{2\sqrt{3}}}{3}$

20．（1）已知a，b，c均为正实数，且a+b+c=1，求证：$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥9；
（2）已知a＞b＞c，且a+b+c=0，求证：$\sqrt{{b}^{2}-ac}$＜$\sqrt{3}$a．

17．已知：数列{a_n}，{b_n}中，a₁=0，b₁=1，且当n∈N^*时，a_n，b_n，a_n+1成等差数列，b_n，a_n+1，b_n+1成等比数列；
（1）求数列{a_n}，{b_n}的通项公式；
（2）求最小自然数k，使得当n≥k时，对任意实数λ∈[0，1]，不等式（2λ-3）b_n≥（2λ-4）a_n+λ-3恒成立．

4．记${\left.{\overline{{a_n}{a_{n-1}}{a_{n-2}}…{a_1}{a_0}}}\right|_m}$=a₀+a₁×m+…+a_n-1×m^n-1+a_n×mⁿ，其中n≤m，m、n均为正整数，a_k∈{0，1，2，…，m-1}（k=0，1，2，…，n）且a_n≠0；
（1）计算${\left.{\overline{2016}}\right|_7}$=699；
（2）设集合A（m，n）=$\left\{{{{\left.{\left.x\right|x=\overline{{a_n}{a_{n-1}}{a_{n-2}}…{a_1}{a_0}}}\right|}_m}}\right\}$，则A（m，n）中所有元素之和为$\frac{{（{{m^{n+1}}+{m^n}-1}）（{{m^{n+1}}-{m^n}}）}}{2}$．

14．已知椭圆$\frac{x^2}{4}$+y²=1，A，B，C，D为椭圆上四个动点，且AC，BD相交于原点O，设A（x₁，y₁），B（x₂，y₂）满足$\frac{{{y_1}{y_2}}}{{\overrightarrow{OA}•\overrightarrow{OB}}}$=$\frac{1}{5}$．
（1）求证：$\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{0}$；
（2）k_AB+k_BC的值是否为定值，若是，请求出此定值，并求出四边形ABCD面积的最大值，否则，请说明理由．

1．已知函数f（x）=ln（x²+1），g（x）=$\frac{1}{{x}^{2}-1}$+a．
（1）若f（x）的一个极值点到直线l：2$\sqrt{2}$x+y+a+5=0的距离为1，求a的值；
（2）求方程f（x）=g（x）的根的个数．

18．已知函数f（x）=$\left\{\begin{array}{l}{1-|x|，（x≤1）}\\{{x}^{2}-4x+3，（x＞1）}\end{array}\right.$，若f（f（m））≥0，则实数m的取值范围是（　　）

[-2，2]∪[4，+∞）

[-2，2+$\sqrt{2}$]

[-2，2+$\sqrt{2}$]∪[4，+∞）

19．已知函数f（x）=x+$\frac{1}{x}$．
（I）判断函数的奇偶性，并加以证明；
（II）用定义证明f（x）在（0，1）上是减函数；
（III）函数f（x）在（-1，0）上的单调性如何？（直接写出答案，不要求写证明过程）．