题目内容
13．设z=$\frac{3}{2}$x+y，其中x，y满足$\left\{\begin{array}{l}x+2y≥0\\ x-y≤0\\ 0≤y≤k.\end{array}$，若z的最大值为6，则z=$\frac{3}{2}$x+y的最小值为$-\frac{24}{5}$．分析 画出可行域，求出目标函数的最大值为6时，k的值，利用目标函数的几何意义求解目标函数的最小值．
解答 解：如图，$\frac{3}{2}x+y=6$过点A时取得最大值，
由$\left\{\begin{array}{l}{y=k}\\{x-y=0}\end{array}\right.$，可得（k，k），$k=\frac{12}{5}$．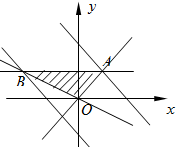
在点B处取得最小值，B点在直线x+2y=0上，由$\left\{\begin{array}{l}{y=\frac{12}{5}}\\{x+2y=0}\end{array}\right.$．可得：
$B（-\frac{24}{5}，\frac{12}{5}）$，
∴${z_{min}}=\frac{3}{2}x+y=-\frac{24}{5}$．
故答案为：$-\frac{24}{5}$．
点评 本题考查线性规划的简单应用，考查转化思想以及计算能力．
练习册系列答案
相关题目
18．已知函数f（x）=$\left\{\begin{array}{l}{1-|x|，（x≤1）}\\{{x}^{2}-4x+3，（x＞1）}\end{array}\right.$，若f（f（m））≥0，则实数m的取值范围是（ ）
| A． | [-2，2] | B． | [-2，2]∪[4，+∞） | C． | [-2，2+$\sqrt{2}$] | D． | [-2，2+$\sqrt{2}$]∪[4，+∞） |
5．
如图所示，点A、B、C是圆O上的三点，线段OC与线段AB交于圆内一点M，若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$，（m＞0，n＞0），m+n=2，则∠AOB的最小值为（ ）
如图所示，点A、B、C是圆O上的三点，线段OC与线段AB交于圆内一点M，若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$，（m＞0，n＞0），m+n=2，则∠AOB的最小值为（ ）| A． | $\frac{2π}{3}$ | B． | $\frac{π}{2}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{6}$ |