题目内容
9.在平面直角坐标系xOy中,已知△ABC顶点A(-4,0)和C(4,0)顶点B在椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1上,则$\frac{sinA+sinC}{sin(A+C)}$=( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
分析 由题意画出图形,求出椭圆的长轴及焦距长,再由正弦定理把$\frac{sinA+sinC}{sin(A+C)}$转化为三角形边的关系得答案.
解答 解:由椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1,得c=4,
则A(-4,0)和C(4,0)为椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1的两个焦点.
∵B在椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1上,
∴a+c=10,b=8.
$\frac{sinA+sinC}{sin(A+C)}$=$\frac{sinA+sinC}{sinB}=\frac{a+c}{b}$=$\frac{10}{8}=\frac{5}{4}$.
故选:D.
点评 本题考查椭圆的简单性质,考查了正弦定理及椭圆定义的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知i是虚数单位,则复数$z={({\frac{1+i}{{\sqrt{2}}}})^{2017}}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.下列命题中的真命题为( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使得$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知随机变量ξ服从正态分布N(1,σ2),若P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| C. | “φ=$\frac{3π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 | |
| D. | 函数y=f(1+x)与函数y=f(1-x)的图象关于直线x=1对称 |
14.等差数列{an}满足a1=1,a2+a3=3,则a1+a2+a3+a4+a5+a6+a7=( )
| A. | 7 | B. | 14 | C. | 21 | D. | 28 |
18.若平面区域$\left\{\begin{array}{l}x+y-3≥0\\ 2x-y-3≤0\\ x-2y+3≥0\end{array}\right.$夹在两条平行直线之间,则这两条平行直线间的距离的最小值是( )
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{5}$ |
19.已知p:a>|b|,q:a2>b2,则下列结论正确的是( )
| A. | p是q的充分不必要条件 | B. | p是q的必要不充分条件 | ||
| C. | p是q的既不充分也不必要条件 | D. | p是q的充要条件 |
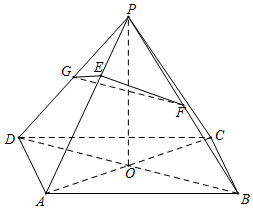 四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.
四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.