题目内容
18.若平面区域$\left\{\begin{array}{l}x+y-3≥0\\ 2x-y-3≤0\\ x-2y+3≥0\end{array}\right.$夹在两条平行直线之间,则这两条平行直线间的距离的最小值是( )| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{5}$ |
分析 作出平面区域,找出距离最近的平行线的位置,求出直线方程,再计算距离.
解答 解:作出平面区域如图所示: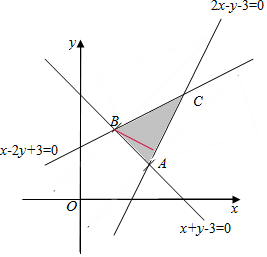
可行域是等腰三角形,平面区域$\left\{\begin{array}{l}x+y-3≥0\\ 2x-y-3≤0\\ x-2y+3≥0\end{array}\right.$夹在两条平行直线之间,则这两条平行直线间的距离的最小值是B到AC的距离,
联立方程组$\left\{\begin{array}{l}{x+y-3=0}\\{x-2y+3=0}\end{array}\right.$,解得B(1,2).
∴平行线间的距离的最小值为d=$\frac{|2×1-2-3|}{\sqrt{{2}^{2}+{1}^{2}}}$=$\frac{3\sqrt{5}}{5}$,
故选:A.
点评 本题考查了平面区域的作法,距离公式的应用,考查转化思想以及计算能力,属于中档题.

练习册系列答案
相关题目
8.在复平面内复数z=$\frac{3+4i}{1-i}$(i为虚数单位)对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.在平面直角坐标系xOy中,已知△ABC顶点A(-4,0)和C(4,0)顶点B在椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1上,则$\frac{sinA+sinC}{sin(A+C)}$=( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
13.已知等比数列{an}的前n项和Sn=2n-a,则数列{log2an}的前10项和等于( )
| A. | 1023 | B. | 55 | C. | 45 | D. | 35 |
7.已知复数z=$\frac{2-i}{2+i}$-$\frac{2+i}{2-i}$,则z=( )
| A. | $\frac{6}{5}$i | B. | $\frac{8i}{5}$ | C. | -$\frac{8i}{5}$ | D. | -$\frac{6}{5}$i |
8.若样本平均数为$\overline{x}$,总体平均数为μ,则( )
| A. | $\overline{x}$=μ | B. | $\overline{x}$≈μ | C. | μ是$\overline{x}$的估计值 | D. | $\overline{x}$是μ的估计值 |