题目内容
14.等差数列{an}满足a1=1,a2+a3=3,则a1+a2+a3+a4+a5+a6+a7=( )| A. | 7 | B. | 14 | C. | 21 | D. | 28 |
分析 利用等差数列通项公式求出公差,由此利用等差数列前n项和公式能求出结果.
解答 解:∵等差数列{an}满足a1=1,a2+a3=3,
∴1+d+1+2d=3,解得d=$\frac{1}{3}$,
∴a1+a2+a3+a4+a5+a6+a7
=7a1+$\frac{7×6}{2}d$=7+7=14.
故选:B.
点评 本题考查等差数列的前7项和的求法,是基础题,解题时要认真审题,注意等差数列的性质合理运用.

练习册系列答案
相关题目
9.在平面直角坐标系xOy中,已知△ABC顶点A(-4,0)和C(4,0)顶点B在椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1上,则$\frac{sinA+sinC}{sin(A+C)}$=( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
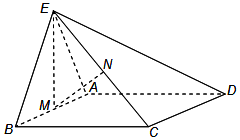 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点,N是CE的中点.