题目内容
已知f(x)是定义在集合M上的函数,若区间D⊆M,且对任意x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭.
(1)判断函数f(x)=x+
在定义域上是否封闭,并说明理由;
(2)若函数g(x)=
在区间[3,10]上封闭,求实数a的取值范围.
(1)判断函数f(x)=x+
| 2x-1 |
(2)若函数g(x)=
| 3x+a |
| x+1 |
考点:函数的值域,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)先求出函数的定义域,再求出函数的值域,从而得出函数是否封闭;(2)由题意得不等式组,解出即可.
解答:
解:(1)函数f(x)的定义域是:{x|x≥
},
令
=t,∴x=
,(t≥0),
∴f(x)=
+t=
(t+1)2≥
,
∴函数f(x)=x+
在定义域上封闭;
(2)g(x)=3+
,
由题意得:3≤3+
≤10,
∴
,解得:3≤a≤31.
| 1 |
| 2 |
令
| 2x-1 |
| t2+1 |
| 2 |
∴f(x)=
| t2+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)=x+
| 2x-1 |
(2)g(x)=3+
| a-3 |
| x+1 |
由题意得:3≤3+
| a-3 |
| x+1 |
∴
|
点评:本题考查了函数的定义域,值域问题,考查了新定义问题,是一道中档题.

练习册系列答案
相关题目
若奇函数f(x)在区间[3,7]上是减函数且有最大值4,则f(x)在区间[-7,-3]上是( )
| A、增函数且最小值为-4 |
| B、增函数且最大值为-4 |
| C、减函数且最小值为-4 |
| D、减函数且最大值为-4 |
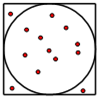 某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计出的圆周率π的值为
某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计出的圆周率π的值为