题目内容
根据下列几何体的三视图,则它的体积V= .


考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:三视图中长对正,高对齐,宽相等.直观图为由圆锥与圆柱组合体,利用体积公式,可得体积.
解答:
解:直观图为由圆锥与圆柱组合体,其中圆锥底面r=2,高h=2,母线长l=2
,圆柱的高为2.
则V=π•22•2+
•π•22•2=
.
故答案为:
.
| 2 |
则V=π•22•2+
| 1 |
| 3 |
| 32π |
| 3 |
故答案为:
| 32π |
| 3 |
点评:考查了学生的空间想象力,及三视图中长对正,高对齐,宽相等的知识,确定直观图是关键.

练习册系列答案
相关题目
下列给出的赋值语句中正确的是( )
| A、4=M | B、M=-M |
| C、B=A-3 | D、x+y=0 |
方程x2-px+6=0的解集为M,方程x2+6x-q=0的解集为N,且M∩N={2},那么p+q=( )
| A、21 | B、8 | C、6 | D、7 |
[x]表示不超过x的最大整数,函数f(x)=|x|-[x]
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
①f(x)的定义域为R;
②f(x)的值域为(0,1];
③f(x)是偶函数;
④f(x)不是周期函数;
⑤f(x)的单调增区间为(k,k+1)(k∈N).
上面的结论正确的个数是( )
| A、3 | B、2 | C、1 | D、0 |
已知等差数列{an}的前n项和Sn,满足Sn=-
n2+2n,则Sn的最大值为( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
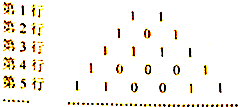 将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是
将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是