题目内容
设函数f(x)=sin(2x+
)+
(x∈R).
(1)求f(x)的最小正周期及区间[0,π]上的单调递减区间;
(2)若函数y=f(x)的图象向右平移
个单位,再向上平移
个单位,得到函数y=g(x)的图象,求y=g(x)在[0,
]上的最大值.
| π |
| 3 |
| ||
| 2 |
(1)求f(x)的最小正周期及区间[0,π]上的单调递减区间;
(2)若函数y=f(x)的图象向右平移
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
考点:三角函数的周期性及其求法,正弦函数的单调性,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)由f(x)的解析式求得f(x)的最小正周期;令2kπ+
≤2x+
≤2kπ+
,求得x的范围,可得函数的减区间;再根据x∈[0,π],进一步确定函数的单调递减区间.
(2)由题意利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)=f(x-
)+
=sin(2x-
)+
,由x∈[0,
]时,利用正弦函数的定义域和值域,求得g(x)在[0,
]上的最大值.
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
(2)由题意利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)=f(x-
| π |
| 4 |
| ||
| 2 |
| π |
| 6 |
| 3 |
| π |
| 4 |
| π |
| 4 |
解答:
解:(1)f(x)=sin(2x+
)+
,故f(x)的最小正周期T=
=π.
令2kπ+
≤2x+
≤2kπ+
,求得kπ+
≤x≤kπ+
,k∈z,可得函数的减区间为[kπ+
,kπ+
],k∈z.
再根据x∈[0,π],可得函数在区间[0,π]上的单调递减区间为[
,
].
(2)由题意g(x)=f(x-
)+
=sin[2(x-
)+
]+
=sin(2x-
)+
,
当x∈[0,
]时,2x-
∈[-
,
],由于g(x)是[0,
]上的增函数,
∴g(x)max=g(
)=
.
| π |
| 3 |
| ||
| 2 |
| 2π |
| 2 |
令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
再根据x∈[0,π],可得函数在区间[0,π]上的单调递减区间为[
| π |
| 12 |
| 7π |
| 12 |
(2)由题意g(x)=f(x-
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 3 |
| 3 |
| π |
| 6 |
| 3 |
当x∈[0,
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
∴g(x)max=g(
| π |
| 4 |
3
| ||
| 2 |
点评:本题主要考查函数y=Asin(ωx+φ)的周期性、及其的图象变换规律,正弦函数的单调性、定义域和值域,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设{an}是由正数组成的等差数列,{bn}是由正数组成的等比数列,且a1=b1,a2003=b2003,则必有( )
| A、a1002>b1002 |
| B、a1002=b1002 |
| C、a1002≥b1002 |
| D、a1002≤b1002 |
下列结论正确的是( )
| A、命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4=0” |
| B、“x=4”是“x2-3x-4=0”的充分不必要条件 |
| C、已知命题p“若m>0,则方程x2+x-m=0有实根”,则命题p的否定¬p为真命题 |
| D、命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2=0,则m≠0或n≠0” |
b>0是函数f(x)=x2+bx+c在[0,+∞)单调的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
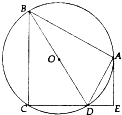 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.