Question

△ABC中，BC=a，CA=b，以边AB为一边长向外作正方体ABEF，O为正方形ABEF的中心，M，N分别为边BC、CA的中点．当∠BCA变化时，求OM+ON的最大值．

Answer 1

考点：正弦定理的应用

专题：解三角形

分析：如图所示，在△OBM中，设AB=c，∠ABC=β．在△OBM中，由余弦定理得：
OM²=(

2

2

c)2+(

1

2

a)2-2×

2

2

c×

1

2

a•cos(

π

4

+β)=

1

2

c2+

1

4

a2-

1

2

ac(cosβ-sinβ)．
在△ABC中，由余弦定理和正弦定理可得：cosβ=

a2+c2-b2

2ac

，c²=a²+b²-2abcosC，

b

sinβ

=

c

sinC

，
得到OM²=

1

2

b2+

1

4

a2+

2

2

absin(C-

π

4

)．同理可得：ON2=

1

2

a2+

1

4

b2+

2

2

sin(C-

π

4

)．
∴当C=

3π

4

时，(OM2)max=

1

2

b2+

1

4

a2+

2

2

ab，(ON2)max=

1

2

a2+

1

4

b2+

2

2

ab．即可得出．

解答： 解：如图所示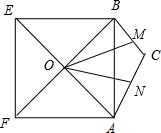，在△OBM中，设AB=c，∠ABC=β．
在△OBM中，由余弦定理得：
OM²=(

2

2

c)2+(

1

2

a)2-2×

2

2

c×

1

2

a•cos(

π

4

+β)
=

1

2

c2+

1

4

a2-

1

2

ac(cosβ-sinβ)．
在△ABC中，由余弦定理和正弦定理可得：cosβ=

a2+c2-b2

2ac

，c²=a²+b²-2abcosC，

b

sinβ

=

c

sinC

，
得到OM²=

1

2

c2+

1

4

a2-

1

2

ac(

a2+c2-b2

2ac

-

bsinC

c

)
=

c2+b2+2absinC

4

=

a2+b2-2abcosC+b2+2absinC

4

=

1

2

b2+

1

4

a2+

2

2

absin(C-

π

4

)．
同理可得：ON2=

1

2

a2+

1

4

b2+

2

2

sin(C-

π

4

)．
∴当C=

3π

4

时，(OM2)max=

1

2

b2+

1

4

a2+

2

2

ab，(ON2)max=

1

2

a2+

1

4

b2+

2

2

ab．
（OM+ON）_max=

1

2

a+

2

2

b+

1

2

b+

2

2

a=

1+ 2

2

(a+b)．

点评：本题考查了正弦定理和余弦定理的应用，考查了推理能力和计算能力，属于难题．