题目内容
设△ABC的内角A,B,C的对边分别为a,b,c,且(a+b+c)(a-b+c)=3ac.
(I)求B
(Ⅱ)若f(x)=
-sinωx-2
sin2
的图象的一个对称中心到最近的对称轴的距离为π,求f(A)的值域.
(I)求B
(Ⅱ)若f(x)=
| 3 |
| 3 |
| ωx |
| 2 |
考点:余弦定理,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:解三角形
分析:(1)根据已知等式求得cosB,进而求得B.
(2)利用二倍角公式对函数解析式进行化简,根据函数的周期求得ω,得到函数解析式,根据A的范围确定f(A)的范围.
(2)利用二倍角公式对函数解析式进行化简,根据函数的周期求得ω,得到函数解析式,根据A的范围确定f(A)的范围.
解答:
解:(1)(a+b+c)(a-b+c)=3ac.
∴
=
,
∴cosB=
,B=
.
(2)f(x)=
-sinωx-2
sin2
=
-sinωx-2
•
=2cos(ωx+
),
由题意知函数f(x)的周期为4π,
∴ω=
=
,
∴f(x)=2cos(
+
),
∴f(A)=2cos(
+
),
∵0<A<
,
∴
<
+
<
,
∴0<cos(
+
)<
,
∴0<f(A)<
,
∴f(A)的值域为(0,
).
∴
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
∴cosB=
| 1 |
| 2 |
| π |
| 3 |
(2)f(x)=
| 3 |
| 3 |
| ωx |
| 2 |
| 3 |
| 3 |
| 1-cosωx |
| 2 |
| π |
| 6 |
由题意知函数f(x)的周期为4π,
∴ω=
| 2π |
| T |
| 1 |
| 2 |
∴f(x)=2cos(
| π |
| 2 |
| π |
| 6 |
∴f(A)=2cos(
| A |
| 2 |
| π |
| 6 |
∵0<A<
| 2π |
| 3 |
∴
| π |
| 6 |
| A |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴0<cos(
| A |
| 2 |
| π |
| 6 |
| ||
| 2 |
∴0<f(A)<
| 3 |
∴f(A)的值域为(0,
| 3 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.考查了学生综合运用三角函数知识的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆x2+y2+4x-2y+4=0的点到直线y=x-1上的最近距离为( )
A、2
| ||
B、
| ||
C、2
| ||
| D、1 |
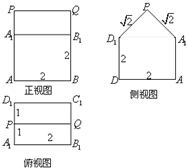 某一几何体的三视图如图所示.按照给出的尺寸(单位:cm):
某一几何体的三视图如图所示.按照给出的尺寸(单位:cm):