题目内容
18．图中阴影部分的面积为$\frac{16}{3}$．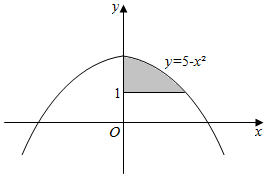
分析 根据题意，所求面积为函数y=5-x2在区间[0，2]上的定积分值，减去有关矩形面积，即可得到本题答案．
解答 解：根据题意，该阴影部分的面积为：${∫}_{0}^{2}$（5-x2）dx-1×2=$5x{|}_{0}^{2}-\frac{1}{3}（{x}^{3}）{|}_{0}^{2}$-2=$\frac{16}{3}$．
故答案为：$\frac{16}{3}$．
点评 本题求曲线围成的曲边图形的面积，着重考查了定积分的几何意义和积分计算公式等知识，属于基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
10．设a=sin$\frac{π}{3}$，b=cos$\frac{π}{3}$，c=$\frac{π}{3}$，d=sin$\frac{π}{2}$，则下列关系中正确的是（ ）
| A． | c＞d＞a＞b | B． | d＞c＞a＞b | C． | c＞d＞b＞a | D． | 以上答案均不对 |