题目内容
10.设a=sin$\frac{π}{3}$,b=cos$\frac{π}{3}$,c=$\frac{π}{3}$,d=sin$\frac{π}{2}$,则下列关系中正确的是( )| A. | c>d>a>b | B. | d>c>a>b | C. | c>d>b>a | D. | 以上答案均不对 |
分析 根据三角函数的定义,进行求值比较大小即可.
解答 解:∵a=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,
b=cos$\frac{π}{3}$=$\frac{1}{2}$,
c=$\frac{π}{3}$>1,
d=sin$\frac{π}{2}$=1,
∴c>d>a>b.
故选:A.
点评 本题主要考查函数值的大小比较,根据特殊角的三角函数值进行比较是解决本题的关键,属于基础题.

练习册系列答案
相关题目
15.用集合表示终边在阴影部分的角a的集合为( )
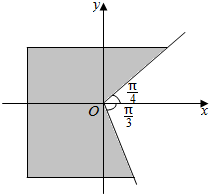

| A. | {a|$\frac{π}{4}$≤a≤$\frac{π}{3}$} | B. | {a|$\frac{π}{4}$≤a≤$\frac{5π}{3}$} | ||
| C. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{π}{3}$,k∈Z} | D. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{5π}{3}$,k∈Z} |
19.已知点(n,an)(n∈N*)在y=ex的图象上,若满足Tn=lna1+lna2+…+lnan>k时n的最小值为5,则k的取值范围是( )
| A. | k<15 | B. | k<10 | C. | 10≤k<15 | D. | 10<k<15 |