题目内容
10.某射击运动员进行射击训练,前三次射击在靶上的着弹点A、B、C刚好是边长为3cm的等边三角形的三个顶点.(Ⅰ) 该运动员前三次射击的成绩(环数)都在区间[7.5,8.5)内,调整一下后,又连打三枪,其成绩(环数)都在区间[9.5,10.5)内.现从这6次射击成绩中随机抽取两次射击的成绩(记为a和b)进行技术分析.求事件“|a-b|>1”的概率.
(Ⅱ)第四次射击时,该运动员瞄准△ABC区域射击(不会打到△ABC外),则此次射击的着弹点距A、B、C的距离都超过1cm的概率为多少?(弹孔大小忽略不计)
分析 (Ⅰ)利用列举法得到所有事件个数,以及满足条件的事件个数,利用古典概型个数求概率;
(Ⅱ)由题意,所求为几何概型概率,所以只要明确三角形区域面积以及射击的着弹点距A、B、C的距离都超过1cm区域面积,利用几何概型公式解答即可.
解答 解:(Ⅰ)前三次射击成绩依次记为x1,x2,x3,后三次成绩依次记为y1,y2,y3,从这6次射击成绩中随机抽取两个,
基本事件是:{x1,x2},{x1,x3},{x2,x3},{y1,y2},{y1,y3},{y2,y3},{x1,y1},{x1,y2},{x1,y3},
{x2,y1},{x2,y2},{x2,y3},},{x3,y1},{x3,y2},{x3,y3},共15个 …(3分)
其中可使|a-b|>1发生的是后9个基本事件.故$P(|a-b|>1)=\frac{9}{15}=\frac{3}{5}$.…(6分)
(Ⅱ)因为着弹点若与A、B、C的距离都超过1cm,则着弹点就不能落在分别以A,B,C为中心,半径为1cm的三个扇形区域内,只能落在扇形外.…(7分)
因为${S}_{△}=\frac{1}{2}×3×3sin60°=\frac{9\sqrt{3}}{4}$ …(8分)
部分的面积为$S'={S}_{△ABC}-3×\frac{1}{2}×{1}^{2}×\frac{π}{3}=\frac{9\sqrt{3}}{4}-\frac{π}{2}$,…(10分)
故所求概率为P=$\frac{S'}{S}=1-\frac{2\sqrt{3}π}{27}$.…(12分)
点评 本题考查了古典概型和几何概型概率求法;明确概率模型,利用相关的公式解答是关键.

练习册系列答案
相关题目
19.已知点(n,an)(n∈N*)在y=ex的图象上,若满足Tn=lna1+lna2+…+lnan>k时n的最小值为5,则k的取值范围是( )
| A. | k<15 | B. | k<10 | C. | 10≤k<15 | D. | 10<k<15 |
15.如图,在四面体ABCD中,设G是CD的中点,则$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BD}+\overrightarrow{BC})$等于( )
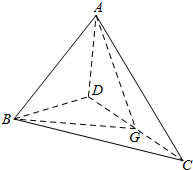

| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BG}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{AG}$ |
19.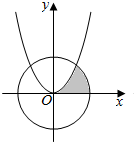 若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
 若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )
若(x2+$\frac{a}{2x}$)6展开式的常数项是15,图中阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,现向圆中投入一颗石子,则此石子恰好落在阴影部分的概率为( )| A. | $\frac{1}{8}$-$\frac{1}{12π}$ | B. | $\frac{1}{8}$+$\frac{1}{12π}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12π}$ |