题目内容
3.函数y=sin2x-3cos2x+2sinxcosx的值域为[-$\sqrt{5}$-1,$\sqrt{5}$-1].分析 根据三角函数的恒等变换,化简函数为y=Asin(ωx+φ)+b的形式,利用正弦函数的有界性求出函数y的值域.
解答 解:函数y=sin2x-3cos2x+2sinxcosx
=$\frac{1-cos2x}{2}$-$\frac{3(1+cos2x)}{2}$+sin2x
=sin2x-2cos2x-1
=$\sqrt{5}$sin(2x+θ)-1,其中tanθ=-2;
∵-1≤sin(2x+θ)≤1,
∴-$\sqrt{5}$-1≤$\sqrt{5}$sin(2x+θ)-1≤$\sqrt{5}$-1,
∴函数y的值域为[-$\sqrt{5}$-1,$\sqrt{5}$-1].
故答案为:[-$\sqrt{5}$-1,$\sqrt{5}$-1].
点评 本题考查了三角函数的化简与求值的应用问题,也考查了三角函数的有界性问题,是基础题目.

练习册系列答案
相关题目
15.用集合表示终边在阴影部分的角a的集合为( )
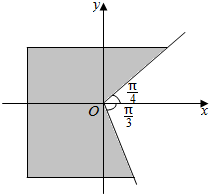

| A. | {a|$\frac{π}{4}$≤a≤$\frac{π}{3}$} | B. | {a|$\frac{π}{4}$≤a≤$\frac{5π}{3}$} | ||
| C. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{π}{3}$,k∈Z} | D. | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{5π}{3}$,k∈Z} |
15.如图,在四面体ABCD中,设G是CD的中点,则$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BD}+\overrightarrow{BC})$等于( )
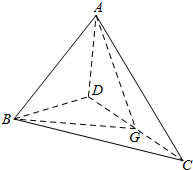

| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BG}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{AG}$ |