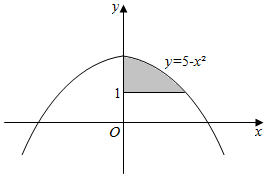
题目内容
6．已知直线a，b和平面α，如果a?α，b?α，且a∥b，求证a∥α分析 利用反证法进行证明即可得到结论．
解答 
证明：（反证法）假设直线a与平面α不平行，则由于a?α，有a与α相交，
设a∩α=P，
若点P∈b上，则a∩b=P与a∥b矛盾．
若点P∉b上，则a与b是异面直线，这与a∥b相矛盾．
于是假设错误，故原命题正确．
即a∥α
点评 本题主要考查线面平行的判定定理的证明，利用反证法是解决本题的关键．
练习册系列答案
相关题目
15．用集合表示终边在阴影部分的角a的集合为（ ）
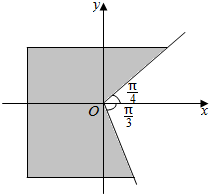
| A． | {a|$\frac{π}{4}$≤a≤$\frac{π}{3}$} | B． | {a|$\frac{π}{4}$≤a≤$\frac{5π}{3}$} | ||
| C． | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{π}{3}$，k∈Z} | D． | {a|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{5π}{3}$，k∈Z} |