题目内容
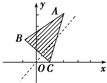在△ABC中，三顶点分别为A（2，4），B（-1，2），C（1，0），点P（x，y）在△ABC内部及其边界上运动，则m=y-x的取值范围为（ ）| A、[1，3] |
| B、[-3，1] |
| C、[-1，3] |
| D、[-3，-1] |
考点：简单线性规划
专题：不等式的解法及应用
分析：根据m的几何意义，平移直线y=x+m，利用数形结合即可求出m的取值范围．
解答：
解：由m=y-x得y=x+m，
平移直线y=x+m，由图象可知当直线y=x+m经过点B（-1，2）时，
直线y=x+m的截距最大，此时m最大，此时mmax=2-（-1）=3
直线y=x+m经过点C（1，0）时，
直线y=x+m的截距最小，此时m最小，mmin=0-1=-1．
即-1≤m≤3，即m∈[-1，3]．
故选：C
平移直线y=x+m，由图象可知当直线y=x+m经过点B（-1，2）时，
直线y=x+m的截距最大，此时m最大，此时mmax=2-（-1）=3
直线y=x+m经过点C（1，0）时，
直线y=x+m的截距最小，此时m最小，mmin=0-1=-1．
即-1≤m≤3，即m∈[-1，3]．
故选：C
点评：本题主要考查线性规划的应用，利用m的几何意义，通过直线平移是解决本题的关键．
练习册系列答案
相关题目
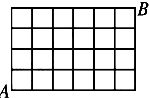某市有7条南北向街道，5条东西向街道．图中共有m个矩形，从A点走到B点最短路线的走法有n种，则m，n的值分别为（ ）| A、m=90，n=210 |
| B、m=210，n=210 |
| C、m=210，n=792 |
| D、m=90，n=792 |
下列有关命题说法正确的是（ ）
A、命题p：“存在x∈R，sinx+cosx=
| ||
| B、“a=1”是“函数f（x）=cos2ax-sin2ax的周期T=π”的充分必要条件 | ||
| C、命题“存在x∈R，使得x2+x+1=0”的否定是：“对任意x∈R，x2+x+1≥0” | ||
D、命题“若tanα≠1，则α≠
|
若直线x-y+2=0与圆C：（x-3）2+（y-3）2=4相交于A、B两点，则
•
的值为（ ）
| CA |
| CB |
| A、-1 | B、0 | C、1 | D、6 |