题目内容
“2a＞2b”是“lga＞lgb”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：由2a＞2b是否得出lga＞lgb？判定充分性；由lga＞lgb是否推出2a＞2b？判定必要性是否成立．
解答：
解：∵2a＞2b等价于a＞b，
当0≥a＞b或a＞0≥b时，lga＞lgb不成立；
∴充分性不成立；
又∵lga＞lgb等价于a＞b＞0，能得出2a＞2b；
∴必要性成立；
∴“2a＞2b”是“lga＞lgb”的必要不充分条件．
故选：B．
当0≥a＞b或a＞0≥b时，lga＞lgb不成立；
∴充分性不成立；
又∵lga＞lgb等价于a＞b＞0，能得出2a＞2b；
∴必要性成立；
∴“2a＞2b”是“lga＞lgb”的必要不充分条件．
故选：B．
点评：本题考查了充分与必要条件的判定问题，解题时需要判定充分性是否成立，必要性是否成立，是基础题．
练习册系列答案
相关题目
若a＞b，则下列不等式成立的是（ ）
| A、lna＞lnb | ||||||
| B、0.3a＞0.3b | ||||||
C、a
| ||||||
D、
|
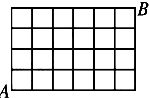某市有7条南北向街道，5条东西向街道．图中共有m个矩形，从A点走到B点最短路线的走法有n种，则m，n的值分别为（ ）| A、m=90，n=210 |
| B、m=210，n=210 |
| C、m=210，n=792 |
| D、m=90，n=792 |
下列说法正确的是（ ）
| A、经过定点P0（x0，y0）的直线都可以用方程y-y0=k（x-x0）表示． | ||||
B、经过不同两点P1（x1，y1），P2（x2，y2）的直线都可以用方程
| ||||
| C、经过定点P0（0，b）且斜率存在的直线都可以用方程y=kx+b表示． | ||||
D、不过原点的直线都可以用方程
|
下列有关命题说法正确的是（ ）
A、命题p：“存在x∈R，sinx+cosx=
| ||
| B、“a=1”是“函数f（x）=cos2ax-sin2ax的周期T=π”的充分必要条件 | ||
| C、命题“存在x∈R，使得x2+x+1=0”的否定是：“对任意x∈R，x2+x+1≥0” | ||
D、命题“若tanα≠1，则α≠
|