题目内容
已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”,下列函数中,有“巧值点”的函数的个数是( )
①f(x)=x2,②f(x)=e-x,③f(x)=lnx,④f(x)=tanx,⑤f(x)=x+
.
①f(x)=x2,②f(x)=e-x,③f(x)=lnx,④f(x)=tanx,⑤f(x)=x+
| 1 |
| x |
| A、2 | B、3 | C、4 | D、5 |
考点:命题的真假判断与应用
专题:新定义
分析:根据“巧值点”的定义,对①②③④⑤五个命题逐一判断即可得到答案.
解答:
解:①中的函数f(x)=x2,f′(x)=2x.要使f(x)=f′(x),则x2=2x,解得x=0或2,可见函数有巧值点;
对于②中的函数,要使f(x)=f′(x),则e-x=-e-x,由对任意的x,有e-x>0,可知方程无解,原函数没有巧值点;
对于③中的函数,要使f(x)=f′(x),则lnx=
,

由函数f(x)=lnx与y=
的图象知,它们有交点,因此方程有解,原函数有巧值点;
对于④中的函数,要使f(x)=f′(x),则tanx=
,即sinxcosx=1,sin2x=2,显然无解,原函数没有巧值点;
对于⑤中的函数,要使f(x)=f′(x),则x+
=1-
,即x3-x2+x+1=0,
设函数g(x)=x3-x2+x+1,g′(x)=3x2+2x+1>0且g(-1)<0,g(0)>0,
显然函数g(x)在(-1,0)上有零点,原函数有巧值点.
故有“巧值点”的函数为①③⑤,共3个.
故选:B.
对于②中的函数,要使f(x)=f′(x),则e-x=-e-x,由对任意的x,有e-x>0,可知方程无解,原函数没有巧值点;
对于③中的函数,要使f(x)=f′(x),则lnx=
| 1 |
| x |

由函数f(x)=lnx与y=
| 1 |
| x |
对于④中的函数,要使f(x)=f′(x),则tanx=
| 1 |
| cos2x |
对于⑤中的函数,要使f(x)=f′(x),则x+
| 1 |
| x |
| 1 |
| x2 |
设函数g(x)=x3-x2+x+1,g′(x)=3x2+2x+1>0且g(-1)<0,g(0)>0,
显然函数g(x)在(-1,0)上有零点,原函数有巧值点.
故有“巧值点”的函数为①③⑤,共3个.
故选:B.
点评:本题考查命题的真假判断与应用,考查导数的应用,突出等价转化思想与数形结合思想的考查,属于难题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
给出下列命题:
①若a,b∈R+,a≠b,则a3+b3>a2b+ab2;
②若a,b,c∈R,则a2+b2+c2≥ab+bc+ca;
③若a>0,b>0,a+b=2,则
+
≤
;
④若
,则
;
⑤函数y=
的最小值等于2.
其中正确命题的个数为( )
①若a,b∈R+,a≠b,则a3+b3>a2b+ab2;
②若a,b,c∈R,则a2+b2+c2≥ab+bc+ca;
③若a>0,b>0,a+b=2,则
| a |
| b |
| 2 |
④若
|
|
⑤函数y=
| x2+2014 | ||
|
其中正确命题的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若a>b,则下列不等式成立的是( )
| A、lna>lnb | ||||||
| B、0.3a>0.3b | ||||||
C、a
| ||||||
D、
|
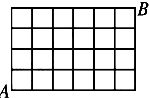 某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )
某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )| A、m=90,n=210 |
| B、m=210,n=210 |
| C、m=210,n=792 |
| D、m=90,n=792 |
下列有关命题说法正确的是( )
A、命题p:“存在x∈R,sinx+cosx=
| ||
| B、“a=1”是“函数f(x)=cos2ax-sin2ax的周期T=π”的充分必要条件 | ||
| C、命题“存在x∈R,使得x2+x+1=0”的否定是:“对任意x∈R,x2+x+1≥0” | ||
D、命题“若tanα≠1,则α≠
|