题目内容
设函数f(x)=lnx.给出下列命题:
①对?0<x1<x2,?x0∈(x1,x2),使得
=
;
②对?x1>0,x2>0,都有f(
)<
;
③当x1>1,x2>1时,都有0<
<1;
④若a<-1,则f(x)>
(x>0).
其中正确命题的序号是 (填上所有正确命题序号)
①对?0<x1<x2,?x0∈(x1,x2),使得
| 1 |
| x0 |
| f(x1)-f(x2) |
| x1-x2 |
②对?x1>0,x2>0,都有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
③当x1>1,x2>1时,都有0<
| f(x1)-f(x2) |
| x1-x2 |
④若a<-1,则f(x)>
| x+a |
| x |
其中正确命题的序号是
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:①利用割线的斜率判断.②利用函数的凸凹性判断.③利用导数的几何意义、以及切线与割线的斜率的关系.④根据不等式构造函数,再转化为利用导数求函数的最值进行证明.
解答:
 解:因为
解:因为
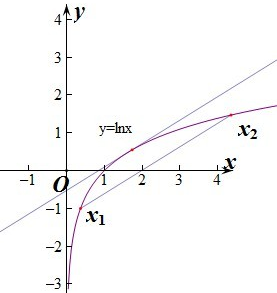
表示过(x1,f(x1))、(x2,f(x2))两点的直线的斜率,
①f′(x)=
,则f′(x0)=
,表示在x=x0处的切线斜率,由图象可知过x1与x2两点的割线和过x0点的切线可能平行,
所以①正确.
②满足f(
)<
的函数为凸函数,
所以②正确.
③因为函数的导数为f′(x)=
,
则当x>1时,0<f′(x)=
<1,
即此时切线的斜率小于1,
所以对应的割线的斜率也小于1,所以0<
<1成立,所以③正确.
④令g(x)=lnx-
=lnx-1-
,(x>0)
则g′(x)=
+
=
,
∵a<-1,∴g′(x)=0时,得x=-a,
当x∈(0,-a)时,g′(x)<0,当x∈(-a,+∞)时,g′(x)>0,
∴x=-a时,函数g(x)取得最小值ln(-a),
由a<-1得,ln(-a)>ln1=0,
∴g(x)=lnx-
>0,即f(x)>
(x>0),所以④正确,
故答案为:①②③④.
 解:因为
解:因为| f(x1)-f(x2) |
| x1-x2 |
①f′(x)=
| 1 |
| x |
| 1 |
| x0 |
所以①正确.
②满足f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
所以②正确.
③因为函数的导数为f′(x)=
| 1 |
| x |
则当x>1时,0<f′(x)=
| 1 |
| x |
即此时切线的斜率小于1,
所以对应的割线的斜率也小于1,所以0<
| f(x1)-f(x2) |
| x1-x2 |
④令g(x)=lnx-
| x+a |
| x |
| a |
| x |
则g′(x)=
| 1 |
| x |
| a |
| x2 |
| x+a |
| x2 |
∵a<-1,∴g′(x)=0时,得x=-a,
当x∈(0,-a)时,g′(x)<0,当x∈(-a,+∞)时,g′(x)>0,
∴x=-a时,函数g(x)取得最小值ln(-a),
由a<-1得,ln(-a)>ln1=0,
∴g(x)=lnx-
| x+a |
| x |
| x+a |
| x |
故答案为:①②③④.
点评:本题主要考查了导数的几何意义以及函数的图象,构造函数法证明不等式成立,以及导数与函数的最值问题,利用数形结合是解决本题的关键,难度很大.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
向量
=(k,12),
=(4,5),
=(10,k),当A,B,C三点共线时k的值为( )
| OA |
| OB |
| OC |
| A、10 | ||
| B、11或-2 | ||
| C、-11或2 | ||
D、
|
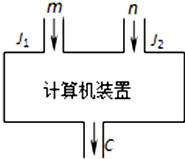 如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:
如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质: