题目内容
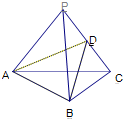已知：如图P为△ABC所在平面外一点，AP=AC，BP=BC，D为PC的中点，求证：PC⊥平面ABD．考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：在△PAC中，由AP=AC且PD=CD，得AD⊥PC，同理，得BD⊥PC，由此能证明PC⊥平面ABD．
解答：
证明：在△PAC中，
∵AP=AC且PD=CD
∴AD⊥PC，（三线合一）
同理，得BD⊥PC
∴PC⊥平面ABD．
∵AP=AC且PD=CD
∴AD⊥PC，（三线合一）
同理，得BD⊥PC
∴PC⊥平面ABD．
点评：本题考查直线与平面垂直的证明，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目