题目内容

求f（x）=x2+
x4
x2-3
（x2＞3）的最小值．
考点：基本不等式在最值问题中的应用
专题：计算题,不等式的解法及应用
分析：设x2-3=t（t＞0），则y=2t+
9
t
+9，利用基本不等式，即可得出结论．
解答： 解：设x2-3=t（t＞0），则y=2t+
9
t
+9≥2
2t•
9
t
+9=9+6
2
，
当且仅当2t=
9
t
，即x2=3+
3
2
2
时，函数的最小值为9+6
2
．
点评：本题考查基本不等式在最值问题中的应用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
lg2x+3lgx-4=0．
若三个数a-4，a+2，26-2a适当排列后构成递增等差数列，求a的值和相应的数列．
设函数y=
x+1，(x≤0)
x2-2，(0＜x＜1)
3，(x≥1)
，画出求函数值y的算法框图．
在△ABC中，a，b，c分别为内角A，B，C所对的边，A＜B＜C，A，B，C成等差数列，公差为θ，且
1
sinA
，
3
2
2sinB
，
1
sinC
也成等差数列．
（Ⅰ）求θ；
（Ⅱ）若a=
6
-
2
，求△ABC的面积．
已知
a
=（2sin（x+
θ
2
），
3
），
b
=（cos（x+
θ
2
），2cos2（x+
θ
2
）），且0≤θ≤π，f（x）=
a
•
b
-
3
，且f（x）为偶函数．
（1）求θ；       
（2）求满足f（x）=1，x∈[-π，π]的x的集合．
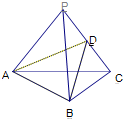已知：如图P为△ABC所在平面外一点，AP=AC，BP=BC，D为PC的中点，求证：PC⊥平面ABD．
已知y=x2-mx-（m+2）的图象与x交点为A、B，则A、B间最短距离是
 
．
关于x的不等式x2-ax+2＞0在（0，5]上恒成立，则a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网