题目内容
解关于x的不等式:2x2-(5a+1)x+2(a2+a)>0.
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:把不等式2x2-(5a+1)x+2(a2+a)>0化为(x-2a)[2x-(a+1)]>0,讨论a的取值,求出不等式的解集.
解答:
解:∵不等式2x2-(5a+1)x+2(a2+a)>0,
可化为(x-2a)[x-
(a+1)]>0,
当2a=
(a+1)时,即a=
时,x≠
,
当2a>
(a+1)时,即a>
时,不等式的解为x>2a或x<
(a+1),
当2a<
(a+1)时,即a<
时,不等式的解为
(a+1)<x<2a,
综上所述,当a>
时,不等式的解集为(-∞,
(a+1)),
当a=
时,不等式的解集为(-∞,
)∪(
,+∞),
当a<
时,不等式的解解集为(
(a+1),2a).
可化为(x-2a)[x-
| 1 |
| 2 |
当2a=
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
当2a>
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
当2a<
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
综上所述,当a>
| 1 |
| 3 |
| 1 |
| 2 |
当a=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
当a<
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查了求一元二次不等式的解法问题,解题时应对字母a进行讨论,是基础题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
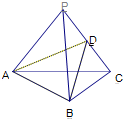 已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD.
已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD. 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OA=6,则tan∠APO的值为
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OA=6,则tan∠APO的值为