题目内容
已知f(x)是定义在R上以2为周期的偶函数,且当0≤x≤1时,f(x)=log
(1-x),则f(-
)= .
| 1 |
| 2 |
| 2011 |
| 4 |
考点:函数的周期性
专题:函数的性质及应用
分析:结合函数的周期性和奇偶性可得:f(-
)=f(
)=f(
-502)=f(
)=log
=2
| 2011 |
| 4 |
| 2011 |
| 4 |
| 2011 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:∵f(x)是定义在R上以2为周期的偶函数,
当0≤x≤1时,f(x)=log
(1-x),
∴f(-
)=f(
)=f(
-502)=f(
)=log
=2,
故答案为:2
当0≤x≤1时,f(x)=log
| 1 |
| 2 |
∴f(-
| 2011 |
| 4 |
| 2011 |
| 4 |
| 2011 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:2
点评:本题考查的知识点是函数奇偶性和函数的周期性,难度不大,转化思路也比较明显,属于基础题.

练习册系列答案
相关题目
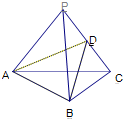 已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD.
已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD.