题目内容
已知函数f(x)=
.
①求函数f(x)的单调区间;
②设g(x)=xf(x)-ax+1,若g(x)在(0,+∞)是存在极值点,求实数a的取值范围.
| ex |
| x |
①求函数f(x)的单调区间;
②设g(x)=xf(x)-ax+1,若g(x)在(0,+∞)是存在极值点,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:①求f′(x),根据f′(x)的符号判断函数的单调区间即可;
②求g′(x),g(x)在(0,+∞)上存在极值点,就是g′(x)=0在(0,+∞)上的实数解,并由g′(x)=0得到x=lna,x>0,所以a>1.
②求g′(x),g(x)在(0,+∞)上存在极值点,就是g′(x)=0在(0,+∞)上的实数解,并由g′(x)=0得到x=lna,x>0,所以a>1.
解答:
解:①f′(x)=
;
∴x∈(-∞,0)和x∈(0,1)时,f′(x)<0;x∈(1,+∞)时,f′(x)>0;
∴函数f(x)的单调减区间是:(-∞,0),(0,1);单调增区间是:[1,+∞);
②g(x)=ex-ax+1,
∴g′(x)=ex-a;
∵g(x)在(0,+∞)上存在极值点;
∴g′(x)=0在(0,+∞)上有实数解;
∴由g′(x)=0得:ex=a,
∴x=lna;
∵x>0,
∴lna>0,
∴a>1;
∴实数a的取值范围为(1,+∞).
| ex(x-1) |
| x2 |
∴x∈(-∞,0)和x∈(0,1)时,f′(x)<0;x∈(1,+∞)时,f′(x)>0;
∴函数f(x)的单调减区间是:(-∞,0),(0,1);单调增区间是:[1,+∞);
②g(x)=ex-ax+1,
∴g′(x)=ex-a;
∵g(x)在(0,+∞)上存在极值点;
∴g′(x)=0在(0,+∞)上有实数解;
∴由g′(x)=0得:ex=a,
∴x=lna;
∵x>0,
∴lna>0,
∴a>1;
∴实数a的取值范围为(1,+∞).
点评:本题考查根据导数符号找单调区间的方法,函数极值点的定义,函数极值点与方程g′(x)=0实数解的关系.

练习册系列答案
相关题目
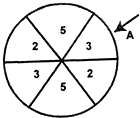 如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).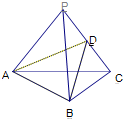 已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD.
已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD.