题目内容
函数f(x)=kx-lnx(k为常数,且k>0),若方程f′(x)•(k-
)=0有唯一的实根x0,则k的取值范围是 .
| 1 |
| f(x) |
考点:函数零点的判定定理
专题:
分析:f′(x)=k-
,则方程f′(x)•(k-
)=0有唯一的实根x0,即(k-
)•(k-
)=0有唯一的实根x0,分类讨论:kx-lnx=x=
,解得k.k-
=0,k-
≠0,解出即可.
| 1 |
| x |
| 1 |
| f(x) |
| 1 |
| x |
| 1 |
| kx-lnx |
| 1 |
| k |
| 1 |
| x |
| 1 |
| kx-lnx |
解答:
解:f′(x)=k-
,
∴方程f′(x)•(k-
)=0有唯一的实根x0,即(k-
)•(k-
)=0有唯一的实根x0,
分类讨论:①kx-lnx=x=
,解得k=1.
②k-
=0,k-
≠0,∴ln
≠1-
,
当k>1时,0<
<1,ln
<0,1-
>0,ln
≠1-
,因此k>1满足题意.
当0<k<1时,
>1,ln
>0,1-
<0,ln
≠1-
,因此0<k<1满足题意.
综上可得:k>0.
| 1 |
| x |
∴方程f′(x)•(k-
| 1 |
| f(x) |
| 1 |
| x |
| 1 |
| kx-lnx |
分类讨论:①kx-lnx=x=
| 1 |
| k |
②k-
| 1 |
| x |
| 1 |
| kx-lnx |
| 1 |
| k |
| 1 |
| k |
当k>1时,0<
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
当0<k<1时,
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
综上可得:k>0.
点评:本题考查了导数的应用、函数的单调性与函数零点的关系,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
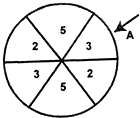 如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).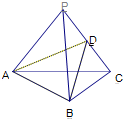 已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD.
已知:如图P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC的中点,求证:PC⊥平面ABD.