题目内容
已知函数f(x)=
.
(1)判断函数f(x)的奇偶性;
(2)函数f(x)在(0,1)上是增函数还是减函数;
(3)设函数g(x)=f(x)•(x+1),求函数g(x)的值域.
| x |
| x2-1 |
(1)判断函数f(x)的奇偶性;
(2)函数f(x)在(0,1)上是增函数还是减函数;
(3)设函数g(x)=f(x)•(x+1),求函数g(x)的值域.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)由f(-x)=-f(x),即可判断函数f(x)的奇偶性;
(2)令0<x1<x2<1,则有f(x2)-f(x1)<0即可判断函数在(0,1)上是增函数还是减函数;
(3)g(x)=1+
,x不能等于1,结合函数的图象,故可求函数g(x)的值域.
(2)令0<x1<x2<1,则有f(x2)-f(x1)<0即可判断函数在(0,1)上是增函数还是减函数;
(3)g(x)=1+
| 1 |
| x-1 |
解答:
解:(1)f(-x)=
=-
=-f(x),故函数f(x)是奇函数;
(2)令0<x1<x2<1,则有f(x2)-f(x1)=
-
=
<0,
故函数f(x)在(0,1)上是减函数;
(3)g(x)=f(x)•(x+1)=
=1+
由x不能等于1,结合函数的图象,故函数g(x)的值域为(-∞,1)∪(1,+∞).
| -x |
| x2-1 |
| x |
| x2-1 |
(2)令0<x1<x2<1,则有f(x2)-f(x1)=
| x2 |
| x22-1 |
| x1 |
| x12-1 |
| (x1-x2)(x1x2+1) |
| (x22-1)(x12-1) |
故函数f(x)在(0,1)上是减函数;
(3)g(x)=f(x)•(x+1)=
| x |
| x-1 |
| 1 |
| x-1 |
由x不能等于1,结合函数的图象,故函数g(x)的值域为(-∞,1)∪(1,+∞).
点评:本题主要考察了函数的性质及应用,属于中档题.

练习册系列答案
相关题目
已知a是函数f(x)=2x-10x的零点,若0<x0<a,则f(x0)的值满足( )
| A、f(x0)=0 |
| B、f(x0)<0 |
| C、f(x0)>0 |
| D、f(x0)的符号不确定 |
函数f(x)=-|x-5|+2x-1的零点所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
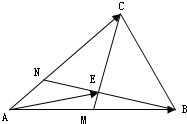 如图所示,在△ABC中,点M是AB的中点,且
如图所示,在△ABC中,点M是AB的中点,且