题目内容
要将两种大小不同的钢板截成A,B,C三种规格,每张钢板可同时截得三种规格的小钢板的块数如表所示:
今需要A,B,C三种规格的成品分别是15,18,27块,至少需要这两种钢板共是 张.
| 规格类型 钢板类型 |
A | B | C |
| 第一 | 2 | 1 | 1 |
| 第二 | 1 | 2 | 3 |
考点:简单线性规划
专题:不等式的解法及应用
分析:根据条件求出约束条件,作出不等式组对于的平面区域,利用数形结合即可得到结论.
解答:
解:设第一种钢板需要x,第二种钢板y张,(x,y∈N)
则由题意得
,目标函数z=x+y,
作出不等式组对于的平面区域如图: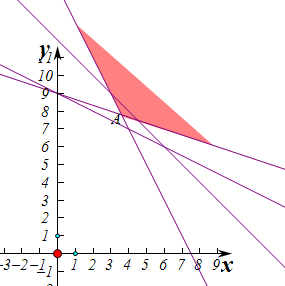
由z=x+y,则y=-x+z,
平移直线y=-x+z,由图象可知当直线y=-x+z,经过点A时,直线y=-x+z的截距最小,此时z最小,
由
,解得
,此时不满足条件,
此时z=
+
=
=11
,
则当z=12时,满足x+y=12,
此时x=12-y,代入约束条件得
,
即
,
∴
≤y≤9,即y=8或9,
当y=8时,x=4,此时z=4+8=12,
当y=9时,x=3,此时z=9+3=12,
此时zmin=12,
故答案为:12
则由题意得
|
作出不等式组对于的平面区域如图:

由z=x+y,则y=-x+z,
平移直线y=-x+z,由图象可知当直线y=-x+z,经过点A时,直线y=-x+z的截距最小,此时z最小,
由
|
|
此时z=
| 18 |
| 5 |
| 39 |
| 5 |
| 57 |
| 5 |
| 2 |
| 5 |
则当z=12时,满足x+y=12,
此时x=12-y,代入约束条件得
|
即
|
∴
| 15 |
| 2 |
当y=8时,x=4,此时z=4+8=12,
当y=9时,x=3,此时z=9+3=12,
此时zmin=12,
故答案为:12
点评:本题主要考查线性规划的应用,利用z的几何意义,利用数形结合是解决本题的关键,由于求出是最优解不满足条件,需要调整最优解,本题有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中真命题是( )
| A、命题“存在x∈R,x2-x-2≥0”的否定是:“不存在x∈R,x2-x-2<0” | ||||||||||
B、线性回归直线
| ||||||||||
C、存在x∈(0,
| ||||||||||
D、函数f(x)=x
|
如图所示程序框图中,输出S=( )
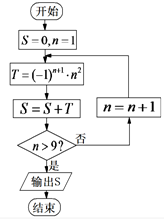

| A、45 | B、-55 |
| C、-66 | D、66 |
下列说法不正确的是( )
| A、方程f(x)=0有实数根?函数y=f(x)有零点 |
| B、函数y=-x2+3x+5有两个零点 |
| C、单调函数至多有一个零点 |
| D、函数f(x)在区间[a,b]上满足f(a)•f(b)<0,则函数f(x)在区间(a,b)内有零点 |

