题目内容
16.在平面直角坐标系xOy中,设直线x-y+m=0(m>0)与圆x2+y2=8交于不同的两点A,B,若圆上存在点C,使得△ABC为等边三角形,则正数m的值为2.分析 先由圆心角与圆周角的关系得到∠AOB=120°,再利用余弦定理得到BD,最后借助于点到直线的距离公式可解得m即可.
解答  解:根据题意画出图形,连接OA,OB,作OD垂直于AB于D点,
解:根据题意画出图形,连接OA,OB,作OD垂直于AB于D点,
因为△ABC为等边三角形,所以∠AOB=120°,由余弦定理知:AB=2$\sqrt{6}$,
故BD=$\sqrt{6}$,所以OD=$\sqrt{2}$,
所以O(0,0)到直线AB的距离$\frac{|m|}{\sqrt{2}}$=$\sqrt{2}$,解得m=±2,
∵m是正数,
∴m的值为2
故答案为2.
点评 本题考查直线与圆的位置关系,考查余弦定理,考查点到直线的距离公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
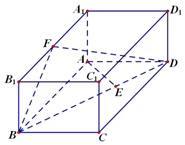 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.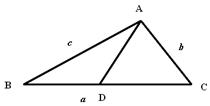 如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.
如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.