题目内容
13.若$sinθ=\frac{3}{5},\frac{5π}{2}<θ<3π$,那么$sin\frac{θ}{2}$=-$\frac{3\sqrt{10}}{10}$.分析 利用同角三角函数的基本关系求得cosθ的值,再利用半角公式求得$sin\frac{θ}{2}$=-$\sqrt{\frac{1-cosθ}{2}}$ 的值.
解答 解:若$sinθ=\frac{3}{5},\frac{5π}{2}<θ<3π$,∴$\frac{θ}{2}$∈( $\frac{5π}{4}$,$\frac{3π}{2}$),cosθ=-$\sqrt{{1-sin}^{2}θ}$=-$\frac{4}{5}$,
那么$sin\frac{θ}{2}$=-$\sqrt{\frac{1-cosθ}{2}}$=-$\frac{3\sqrt{10}}{10}$,
故答案为:-$\frac{3\sqrt{10}}{10}$.
点评 本题主要考查同角三角函数的基本关系,半角公式的应用,属于基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
2.已知A={x|x2-2x-3≤0},B={x|x=2n-1,n∈N*},则A∩B=( )
| A. | {1,3} | B. | {-1,1,3} | C. | {-1,1} | D. | {0,2} |
3.一个长为12m,宽为4m的长方形内部画有一个中国共青团团徽,在长方形内部撒入80粒豆子,恰好有30粒落在团徽区域上,则团徽的面积约为( )
| A. | 16m2 | B. | 30m2 | C. | 18m2 | D. | 24m2 |
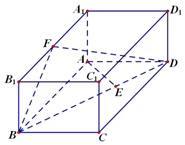 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.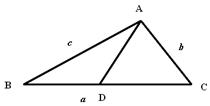 如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.
如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.