题目内容
1.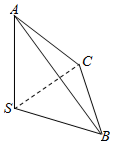 如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 根据二面角的定义作出二面角的平面角,结合三角形的边角关系进行求解即可.
解答 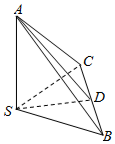 解:∵三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,
解:∵三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,
∴SA⊥平面SBC,且AB=AC=$\sqrt{S{A}^{2}+S{B}^{2}}$,
取BC的中点D,
连接SD,AD,
则SD⊥BC,AD⊥BC,
则∠ADS是二面角A-BC-S的平面角,
设且SA=SB=SC=1,则SD=$\frac{\sqrt{2}}{2}$,
则tan∠ADS=$\frac{SA}{SD}$=$\frac{1}{\frac{\sqrt{2}}{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$,
故选:C
点评 本题主要考查二面角的求解,利用二面角的定义作出二面角的平面角是解决本题的关键.比较基础.

练习册系列答案
相关题目
6.在△ABC中,若$BC=\sqrt{3}$,$AC=\sqrt{2}$,∠B=45°,则∠A=( )
| A. | 60°或120° | B. | 60° | C. | 30°或150° | D. | 30° |
13.已知函数f(x)=$\frac{|x|}{x+2}$,如果关于x的方程f(x)=kx2有四个不同的实数解,则k的取值范围是( )
| A. | k>1 | B. | k≥1 | C. | 0<k<1 | D. | 0<k≤1 |
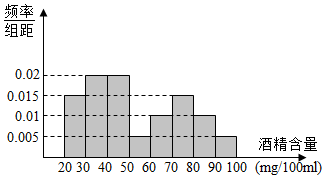 按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.