题目内容
13.已知函数f(x)=2cosxsin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx.①求f(x)的最小值及取得最小值时相应的x值;
②若x∈[$\frac{π}{12}$,$\frac{7π}{12}$].求满足f(x)=1的x值.
分析 ①由三角函数公式化简可得f(x)=2sin(2x+$\frac{π}{3}$),易得函数f(x)的最小值和x值;
②由已知角的范围可得2x+$\frac{π}{3}$∈[$\frac{π}{2}$,$\frac{3π}{2}$],再由sin(2x+$\frac{π}{3}$)=$\frac{1}{2}$可得2x+$\frac{π}{3}$=$\frac{5π}{6}$,解方程可得.
解答 解:①f(x)=2cosxsin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx
=2cosx($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)-$\sqrt{3}$sin2x+sinxcosx
=$\sqrt{3}$(cos2x-sin2x)+2sinxcosx
=$\sqrt{3}$cos2x+sin2x=2sin(2x+$\frac{π}{3}$),
当2x+$\frac{π}{3}$=2kπ-$\frac{π}{2}$即x=kπ-$\frac{5π}{12}$(k∈Z)时,
函数f(x)取最小值-2;
②∵x∈[$\frac{π}{12}$,$\frac{7π}{12}$],∴2x+$\frac{π}{3}$∈[$\frac{π}{2}$,$\frac{3π}{2}$],
由f(x)=2sin(2x+$\frac{π}{3}$)=1可得sin(2x+$\frac{π}{3}$)=$\frac{1}{2}$,
∴2x+$\frac{π}{3}$=$\frac{5π}{6}$,解得x=$\frac{π}{4}$
点评 本题考查三角函数恒等变换及其应用,涉及三角函数的最值,属基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
4.若角α的终边落在直线x+y=0上,则tanα的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
8.不等式组$\left\{\begin{array}{l}{x-y≤0}\\{x+y≥-2}\\{x-2y≥-2}\end{array}\right.$的解集记为D,若(a,b)∈D,则z=2a-3b的最大值是( )
| A. | 1 | B. | 4 | C. | -1 | D. | -4 |
1.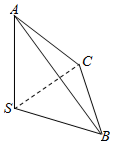 如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
 如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
8.在数列{an}中,a7=16,an-$\frac{1}{2}$an+1=0,则a2的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
6.用边长为120cm的正方形铁皮做一个无盖水箱,先在四周分别截去一个小正方形,然后把四边翻转90°角,再焊接成水箱,则水箱的最大容积为( )
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
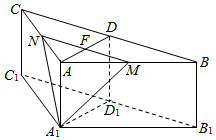 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.